第九章  二次型

一、填空题(每小题2分,共16分)

1 二次型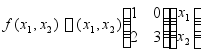的矩阵为                      ．

2 实数域上3阶对称矩阵按合同关系可分为        类．

3 两个元实二次型等价的充分必要条件是                         ．

4  A正定                                          ．

                                          ．

                                          ．

5 某四元二次型有标准形，则其典范形为           ．

6 实二次型)=为正定二次型的充要条件

是                                                  。

7 若是实二次型)的矩阵，则二次型的秩等于的       

  特征根的个数，而           为的正特征根个数与负特征根个数的差。

8 实二次型的标准形是由           和               唯一确定的。

二、判断说明题（先判断正确与错误，再简述理由．每小题5分，共20分）

1．元实二次型的符号差与秩有相同的奇偶性．

2．阶实对称矩阵A若满足，则A正定．

3．A为阶复对称矩阵，则与合同．

4．设A，B分别是阶正定矩阵，则也是正定矩阵．

三、计算题（每小题15分，共60分）

1．用可逆线性替换将二次型化为标准形．写出所用的线性变换及变换矩阵，并求出的正惯性指数与符号差．

2. 已知二次型的秩为2。

(1) 求参数；

(2) 用正交变换将二次型化为标准形，并写出所用的正交变换；

(3) 指出方程表示何种二次曲面。

3．已知二次型通过正交变换化为标准形，求的值及所作的正交变换．

4. 化二次型为标准形，并写出对应的非奇异线性变换。

四、证明题（第小题10分，共20分）

1．A为实对称矩阵，B为对称正定矩阵，证明：存在可逆矩阵T，使

为对角形，．

2．设A为实对称矩阵，且

（1）求A的特征值；

（2）证明A为正定矩阵．