第七章  应力状态和强度理论

§7-1  概述

   简单受力情况：单向拉伸，纯剪(扭)，根据实验建立强度条件。

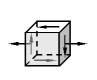    复杂应力状态:

例如：工字钢横力弯曲

    腹板与翼缘交界处：如何建立强度条件，根据还是?

    需要对一点的应力进行深入研究。

  一点的应力状态 ： 构件内，过一点所作各不同截面应力的集合。

§7-2  平面应力状态的应力分析.主应力

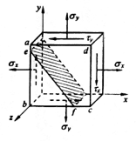平面应力状态(一对平行侧面上无应力，其余面上的应力平行于这对平面)

一、任一斜截面的应力(与无应力平面垂直的平面))

可画平面图

1.符号规定：方位角：(从轴)逆时针正

正应力：拉为正

切应力：使顺时针转为正

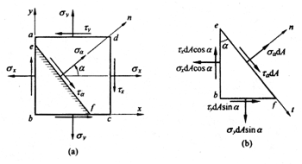2.方法：静力平衡分析法

        微三角块平衡

3结果:

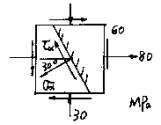4.例题：已知，求，        ——解析法

解：

，

，

轴向左，则，代入公式

二、应力圆——求，的图解法

1、原理

  从上节：

两边平方后相加(第一个方程移项)

   应力圆方程

从数学观点

 ，的轨迹为圆，圆心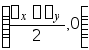，半径，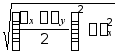     

2、应力圆的绘制及应用

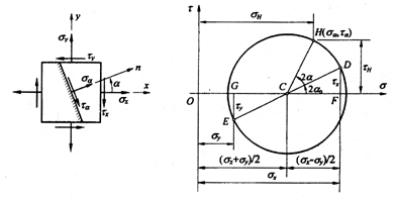
（1）取，坐标(一般省去下标，为，)

（2）面上的应力以点表示，面上的应力以点表示。

(与数值相等，故DF=EG,CD为直径，与坐标轴的交点即为圆心)

（3）连D、E，交坐标轴于C，以C为圆心，或为半径作圆，即得应力圆。

3、应力圆的应用——求面上的应力

    CD转2至CH，点H坐标即为，

4、圆与面的关系(应力圆与微体截面的关系)

（1） 圆上一点坐标=微体一个截面应力值

（2） 圆上两点所夹圆心角=两截面法线夹角的两倍

（3）对应夹角转向相同

例：求图示单元体指定截面的应力。

解

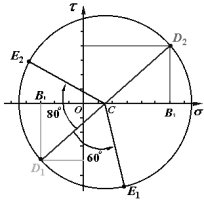
三、主应力与主平面

1、平面应力状态的极值应力

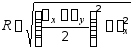
方位：

          (有两个角，由应力圆或微体x面切应力方向判断)

    方位与正应力极值截面成的夹角

2、主应力

    主平面：的面

    主平面单元体：三对互主平面组成的微小六面体

    主应力：主平面上的正应力。以，，表示

例：三个主应力为30MPa、-60 MPa、0

那么：

应力状态分为:

  单向应力状态 ：只有一个主应力不为零 

  二向应力状态：两个主应力不为零

  三向应力状态： 三个主应力都不为零（复杂应力状态）

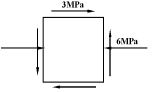
例：求图示单元体的主应力及主平面位置

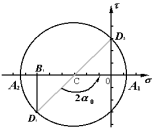解：

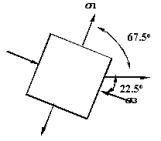
量得

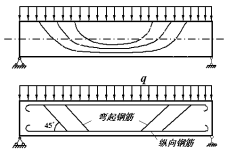
主应力迹线:

根据梁内各点的主应力方向，可在梁的平面内绘制两组曲线。一组曲线各点的切向沿主拉应力方向，另一组沿主压应力方向，两组曲线相互正交。此曲线族称为梁的主应力迹线。钢筋混凝土的主承力钢筋大致沿主应力方向。

§7-3  空间应力状态的概念

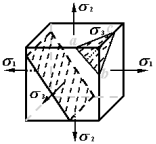    本节研究应力状态的一般形式，并研究所有斜截面应力。

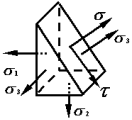
一、三向应力圆

  1.三组特殊平面的应力

    对应于三个应力圆

    (1)平面，由作应力圆

    (2)平面，由作应力圆

    (3)平面，由作应力圆

任意斜截面上的应力对应的点落在三向应力圆的阴影

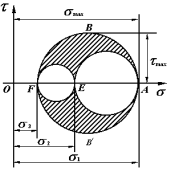
§7-4  应力与应变间的关系

    单向拉伸胡克定律

    纯剪胡克定律

    广义胡克定律：复杂应力状态下，应力和应变关系。

一、各向同性材料的广义胡克定律

    1.对主应力微体(利用叠加原理)

    只有：

        ：

        ：

叠加

    2.非主应力微体

    (线弹性，小变形，与为两组独立应力，叠加原理成立，符号)

    3.平面应力状态：

也可以由表示：

    4.适用范围

     线弹性（胡克定律），小变形，各向同性材料。

§7-5 空间应力状态下的应变能密度

对主应力微体

 1.应变能密度

    单拉：

    复杂应力状态：（比例加载，应变能与加载顺序无关）

代入广义胡克定律

 2.体积与形状改变能密度

    应变能密度能够分解为体积改变能密度与形状改变能密度之和

    体积改变能密度等于与之体积应变相等的三向等应力单元体(其应力为的应变能密度，故

3.形状改变能密度：

§7-6   强度理论及其相当应力

建立强度理论的基本思想

1、问题的提出

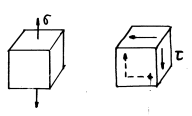
                      单拉            纯剪

   强度条件                      

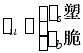
，实验易测。

复杂应力状态可以(简化)由三向主应力微体代表。由实验建立强度条件存在困难：

    （1）.三向加载的实验难于实现。

    （2）很多组合，即使能作实验，工作量也很大。

    （3），与复杂极限应力之间的关系不能把握。

2、研究目的

    利用简单应力状态的实验结果建立复杂应力状态的强度条件

3、研究途径，寻找引起材料破坏的共同规律(找相当应力)

    (认为材料破坏是由某种主要因素引起的，只要这一因素达到一定数值，不论什么应力状态，都会发生破坏)

4、定义：关于材料破坏规律的假说或学说，通常称为强度理论

5、两类破坏形式两类强度理论。

二、脆性断裂强度理论(适用于脆性材料)

1、最大拉压力理论(第一强度理论)

    (认为引起断裂的主要因素是最大拉应力，即仅第一主要应力起作用)

    断裂条件：        ：单拉实验得拉伸强度极限

    强度条件：

    适用：

     (相当应力，讲完第二强度理论再定义)

2、最大伸长线应变理论(第二强度理论)

    (如果三向受压，显然第一强度理论失效)认为断裂的主要因素是最大拉应变达到临界值

    断裂条件       

    左边工作应力引起(压为主)    右边单向拉伸实验获得

    强度条件：

    令相当应力

    强度条件：

    适用      

    实验证实：(1)石、砖等压缩、纵向开裂

              (2)铸铁压缩断裂

              (3)求脆性材料与的关系

    纯剪

直接实验

按第一强度理论    

    按第二强度理论   

如取，通常取  脆性材料

三、塑性屈服强度理论(对塑性材料)

1、最大切应力理论(第三强度理论)

    (认为屈服的主要因素是最大切应力)

    屈服条件   

            工作应力     单拉

    强度条件   (简单，但未考虑的影响)

2、形状改变能密度理论(第四强度理论)

    屈服条件     

    单拉：       

强度条件：

    (第三、四强度理论都应用广泛，第四强度理论更符合试验结果)

求塑性材料与的关系:

    直接实验   

    第三强度理论    

按第四强度理论

    一般取  (塑性材料)

四、小结

    1.相当应力

    强度理论：根据材料的破坏机制，分析材料破坏的主导因素，由此确定复杂应力状态在引起材料破坏方面与单向拉伸应力的相当值，建立定量的强度理论。

    一种常见平面应力状态的相当应力

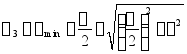
   脆性材料: 如果为正或0，用第一强度理论。 如果为正或负，用第二强度理论。

    塑性材料: , 

    2.强度理论的适用范围

    (1)一般情形

    一、二强度理论适用脆性材料

    三、四强度理论适用于塑性材料。

    (2)工作条件影响

    应力状态：三向等压：脆塑，海底岩石，塑性变形

    三向等拉：塑脆，低碳钢拉伸，滑移线，颈缩，脆断，断面轴线，不成45角。

温度，金属，塑脆，加载速

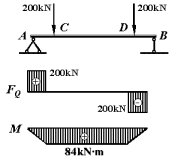例： 工字钢简支梁及所受荷载如图。已知材料的容许应力 ，试由强度计算选择工字钢的型号。

解（1）正应力设计

选用28a号工字钢

（2）切应力校核

28a号工字钢满足强度要求。

（3）主应力校核

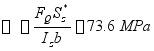
改选32a号