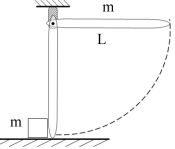
三、刚体定轴转动

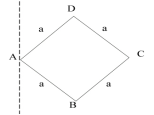
  1．如图所示，在边长为a的正方形的顶点上，分别有质量为m的四个质点，求此系统绕下列轴转动的转动惯量：

   （1）通过A平行于对角线BD的转轴；

   （2）通过A垂直于所在平面的转轴。

2．求半径为R，质量为m的均匀半圆环对于图中所示轴线的转动惯量。

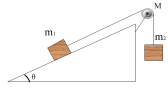
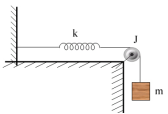
3．如图所示，质量的木块，可沿倾角的斜面滑动，滑动摩擦系数，现在木块由绕过定滑轮的轻绳栓着，绳子的另一端吊着质量的重物，设滑轮为均匀圆盘，质量M=20kg，半径R=0.2m，并设绳子与滑轮间无相对滑动，求重物的加速度和绳子的张力。

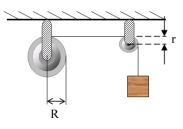
  4．质量为24kg的圆盘轮可绕水平轴转动，一绳缠绕于轮上，另一端通过质量为5kg的圆盘形滑轮悬有10kg的物体，当重物由静止开始下降了0.5m时，求：

  （1）物体的速度；

  （2）绳中的张力，设绳子与滑轮间无相对滑动。

   5．如图所示，滑轮转动惯量为，半径为7cm,物体质量为5kg，由绳与倔强系数的弹簧相连，若绳与滑轮间无相对滑动，滑轮轴上的摩擦忽略不计，求：

  （1）当绳拉直，弹簧无伸长时，使物体由静止而下落的最大距离；

  （2）物体速度达最大值的位置及最大速率。

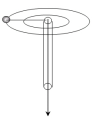
6．将一质量的小球系于轻绳的一端，绳穿过一竖直的管子，一手握管子一手执绳子，先使小球以角速度在半径的水平面上转动，然后将绳子向下拉，使，求小球转动的角速度以及转动动能变化了多少？

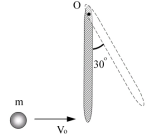
  7．质量为M长为的均匀细棒可绕垂直于棒的一端的水平轴O无摩擦地转动，它原来静止在竖直位置上，如图所示，现有一质量为m的弹性小球沿水平方向飞来，正好在棒的下端与棒相碰，碰撞后从竖直位置摆到最大角处。

  （1）假定碰撞是完全弹性的，计算小球速度的大小；

  （2）碰撞时，小球受到冲量有多大？

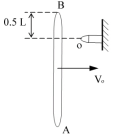
   8．一匀质细杆，长为，质量为M，以水平速度在光滑的水平面内平动时，与前方一固定的支点O发生完全非弹性碰撞。如图所示，求杆与O点碰后绕O点转动的角速度。

   9．两个物体A、B的质量分别为，分别系于两条绳上，这两绳又分别绕在半径为，并且装于同一轴的两个鼓轮上，如图所示。重物在重力作用下运动。设绳子的质量及轴与鼓轮间的摩擦均可忽略不计。试求下列两种情形下的角加速度。

    （1）两个轮盘的质量忽略不计；

（2）小轮质量为，大轮质量为。

10．一均匀细棒长为，质量为m，可绕过一端O的水平轴线在铅直面内转动。棒被拉到水平位置轻轻放开，当它落在铅直位置时，与地面上一静止的物体相碰（如图示），若物体的质量也为m，物体与地面间的摩擦系数为，物体滑动S距离后静止，求棒与物体碰撞后，棒的中点离地面的最高距离为多少？