第2章  网络的正弦稳态分析

    本章要求：

    1. 理解正弦量的特征及其各种表示方法；

2. 理解电路基本定律的相量形式及阻抗；熟练掌握计算正弦交流电路的相量分析法，会画相量图。；

3. 掌握有功功率和功率因数的计算,了解瞬时功率、无功功率和视在功率的概念；

4. 了解正弦交流电路的频率特性，串、并联谐振的条件及特征；

5. 理解提高功率因数的意义和方法。

重点：

1．正弦量的相量表示；

2．正弦交流电路电压与电流关系；

3．正弦交流电路的相量分析法；

4．有功功率和功率因数的计算。

难点：

1．正弦交流电路电压与电流关系的相量表示；

2．正弦交流电路的相量分析法。

2.1 正弦电压与电流

正弦量：随时间按正弦规律做周期变化的量。

正弦量的三要素：幅值、角频率、初相角。

2.1.1周期、频率与角频率

周期T：变化一周所需的时间 （s）

频率f ：         （Hz）

角频率：                     （rad/s）

2.1.2  幅值与有效值

幅值：Im、Um、Em

有效值：与交流热效应相等的直流定义为交流电的有效值。I、U、E

根据

可得

同理：

交流电压、电流表测量数据为有效值，交流设备名牌标注的电压、电流均为有效值。

2.1.3初相位与相位差

相位：反映正弦量变化的进程。

初相位： 表示正弦量在 t = 0时的相位角。给出了观察正弦波的起点或参考点。

相位差 ：两同频率的正弦量之间的初相位之差，反映相位关系。

2.2  正弦量的相量表示法

１. 正弦量的表示方法

波形图、瞬时值表达式、相量表示（实质：用复数表示正弦量）

设A为复数，其表示形式有:

(1)  代数式：A = a + jb

(2)  三角式:

(3)  指数式:  

(4)  极坐标式:

设正弦量:

相量表示:                       相量的模=正弦量的有效值

                                相量辐角=正弦量的初相角

注意：

① 相量只是表示正弦量，而不等于正弦量。

② 只有正弦量才能用相量表示，非正弦量不能用相量表示。

③ 相量的两种表示形式：相量式、相量图。

④ 同频率的正弦量能画在同一相量图上。可不画坐标轴，参考相量画在水平方向。

⑤ 相量的书写方式：模用最大值表示 ，则用符号         ；

                   实际应用中，模多采用有效值，符号：      。

⑥“j”的数学意义和物理意义：虚数单位；

                             旋转 90°因子，                             。

2.3  单一参数的交流电路

2.3.1. 电阻元件的交流电路

1. 电压与电流的关系

① 频率相同； 

②大小关系：         

③相位关系 ：u、i 相位相同，相位差

相量式：

相量图：

2. 功率关系

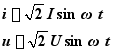(1) 瞬时功率 p ：瞬时电压与瞬时电流的乘积。

结论:   p ≥0 （耗能元件）,且随时间变化。

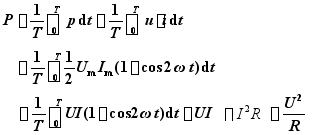(2) 平均功率(有功功率)P：瞬时功率在一个周期内的平均值。 单位：瓦（W）。通常铭牌数据或测量的功率均指有功功率。

2.3.2 电感元件的交流电路

1. 电压与电流的关系

基本关系式：

① 频率相同；

② U =I L ；

③ 电压超前电流90，相位差

定义：感抗                    (Ω)，则

相量式：

相量图：

2. 功率关系

                 ,

(1) 瞬时功率:

(2) 平均功率:

纯电感不消耗能量，只和电源进行能量交换（能量的吞吐)。电感L是储能元件。

(3) 无功功率：用以衡量电感电路中双向能量交换的规模。用瞬时功率达到的最大值表征，即                           ，单位：var。

2.3.3 电容元件的交流电路

1. 电流与电压的关系：

基本关系式：

① 频率相同；

② I =UC ；

③ 电流超前电压90，相位差

定义：容抗                       （Ω），则

相量式：

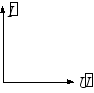相量图：

2.功率关系：

                ，

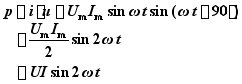(1) 瞬时功率：

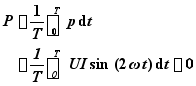
(2) 平均功率：

纯电容不消耗能量，只和电源进行能量交换（能量的吞吐)。电容C是储能元件。

(3) 无功功率：为了同电感电路的无功功率相比较，设               ，则

                   ，                    。无功功率等于瞬时功率达到的最大值。

                             单位：var

2.4   RLC串联的交流电路

1.  电流、电压的关系

(1) 瞬时值表达式

根据KVL可得：

(2)相量法

1)相量式

设          ，则          ，            ，

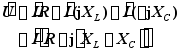
令阻抗                     ，则

可见，Z 的模∣Z∣表示 u、i 的大小关系，辐角（阻抗角） 为 u、i 的相位差。

阻抗模

阻抗角

 由电路参数决定：当 XL >XC  时，  > 0 ，u 超前 i ，电路呈感性；

                  当 XL < XC 时 ， < 0 ， u 滞后 i ，电路呈容性；

                  当 XL = XC 时 ， = 0 ， u、i 同相 ，电路呈电阻性。

注意：Z 是一个复数，不是相量，上面不能加点。

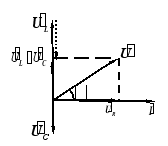
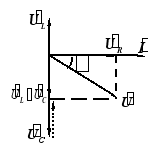2) 相量图

 > 0 感性:                            < 0 容性：

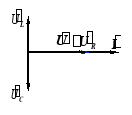 =0 阻性：

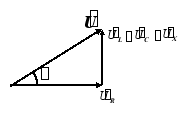
电压三角形：                                由电压三角形可得:

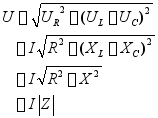
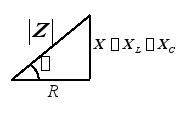
阻抗三角形：                               

电压三角形与阻抗三角形相似。

2.功率关系

(1)  瞬时功率

设

则

第一项为耗能元件上的瞬时功率，第二项为储能元件上的瞬时功率。在每一瞬间，电源提供的功率一部分被耗能元件消耗掉，一部分与储能元件进行能量交换。

(2)  平均功率P （有功功率）

根据电压三角形可得：                             单位: W

(3) 无功功率Q

根据电压三角形可得：                  单位：var

(4)  视在功率 S

                                  单位：V·A

功率三角形：

2.5 阻抗的串联与并联

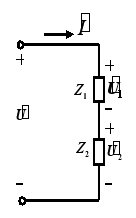2.5.1 阻抗的串联 

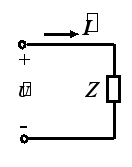                                      可等效为：

等效阻抗             ，则

一般有

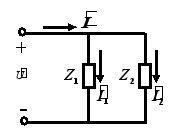
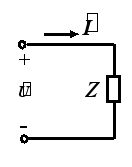2.5.2  阻抗并联

                                       可等效为：

等效阻抗                ，则

一般有

2.8  功率因数的提高

1.功率因数cosφ

由于电源设备的容量是视在功率S = UI，而输出的有功功率却为P = UIcosφ ，因此为了充分利用电源设备的容量,同时也为了减小线路和发电机绕组的损耗，要求提高电路的功率因数。

2.功率因数提高的方法

由于常用负载多为感性负载，所以在感性负载两端并联适当大小的电容可以提高功率因数。并联电容后，电路的总电流减小，总功率因数增大，总的有功功率不变。

并联电容大小为                            。