第六章  简单超静定问题

§6．1超静定结构概述

1. 定义

用静力学平衡方程无法确定全部约束力和内力的结构或结构系统，统称为超静定结构或系统，也称为静不定结构或系统。

2. 静定、超静定结构（系统）

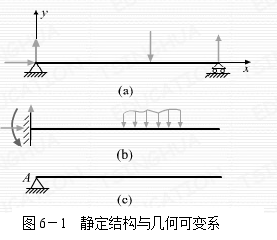
无多余联系的几何不变的承载结构系统，其全部支承反力与内力都可由静力平衡条件求得，此系统称为静定结构或系统。静定结构除了变形外，没有可运动的自由度（图6-1（a、b））

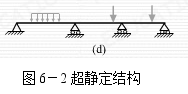如解除简支梁的右端铰支座，或解除悬臂梁固端对转动约束，使之成为铰支座，则此时的梁变成了图6.1（c）的可动机构，是几何可变系不能承受横向载荷。在无多余联系的几何不变的静定系统上增加约束或联系，称为多余约束，并因而产生多余约束反力，则这样的有多余约束的系统，仅利用静力平衡条件无法求得其反力和内力，称为超静定（或静不定）系统。如图6-2所示。

3. 静不定次数的确定

   在超静定问题中，都存在维持平衡所必需的支座或杆件，习惯上称其为“多余”约束。由于多余约束的存在，未知力的数目必然多于独立平衡方程的数目。未知力数目超过独立方程数的数目，称为超静定次数。因此，超静定次数就等于多余约束或多余未知力的数目。

4. 基本静定系（静定基），相当系统

   解除静不定结构的某些约束后得到静定结构，称为原静不定结构的基本静定系（简称静定基）。静定基的选择可根据方便来选取，同一问题可以有不同选择。

在静定基上加上外载荷以及多余约束力的系统称为超静定结构的相当系统。

5.解超静定问题的步骤

(1)    建立相当系统，列静力学平衡方程。

(2)    观察静定基在多余约束处的变形与实际相协调的关系式----建立变形协调方程。

(3)   建立物理方程（如胡克定律，热膨胀规律等）。

(4)    联立静力平衡方程以及根据变形协调方程和物理方程所建立的补充方程，求出未
知力（约束力或内力）。

注意：注意：变形协调条件应使静定基变形与原超静定结构相一致。

§6－2 拉压超静定问题

Ⅰ 拉压超静定问题解法

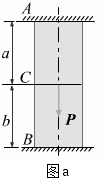
【例2－1】 如图a所示，已知等截面直杆的两端固定，求A，B处的约束反力，。

【解】此结构的约束力个数为2，独立平衡方程数为1，属于一次超静定问题
（1） 静力平衡方程

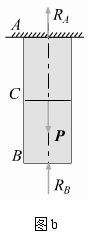如图b所示解除B处约束，即得相应静定基，静定基上除B处给以相应约束力外，还作用有P，。

由得

即      （a）
（2）变形协调方程
    （b）

（3）物理方程
由胡克定律 = ，=  （c）

将（c）式代入（b）式得补充方程

  或             （d）

（4）求解 （a）、（d）式得
，（）
，（）

Ⅱ 装配应力和温度应力

装配应力：由于装配误差使构件尺寸相应变化，引起结构变形而产生的应力。

温度应力：由于温度变化使构件尺寸相应变化，引起结构变形而产生的应力。

温度应力、装配应力问题一般可应用超静定的解法解决。

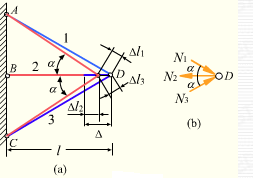【例2-2】图示所示为超静定杆系结构，1，3杆的拉伸刚度为E1A1，2杆的为E2A2，已知中间杆2加工制作时短了，试求三杆在D点铰接在一起后各杆的内力。
【解】图中红线为装配后的位置，蓝线AD、CD为1、3杆装配前的位置，由变形知1、3杆的轴力及为压力，2杆的为张力，D点的受力图如图b。
（1） 静力平衡方程
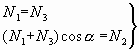             （a）

（2） 变形协调条件

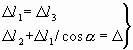      （b）  

（3）物理方程
      （c）

由（b），（c）得补充方程
       （d）
由（a），（d）解得：

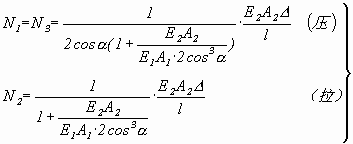
【例2-3】如图所示，等直赶AB的两端分别与刚性支承连接。设两支承间的距离（即杆长）为,杆的横截面积为A， 材料的弹性模量为E，线膨胀系数为。试求温度升高时杆内的温度应力。

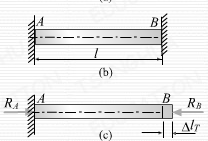【解】1）由静力平衡方程
                （a）

此结构的约束力个数为2，独立平衡方程数为1，属于一次超静定问题
2）变形协调方程
     (b)

是杆件因作用而产生的缩短；是温度上升时的伸长。
3）物理方程
，    （c）

由（c），（b）式得补充方程

即有

应力为

           (d)

结果为正，说明当初设定杆受轴向压力是对的，故该杆的温度应力是压应力。

对于钢杆，，，则当温度升高时，杆内的温度应力由式（d）算得为

（压应力）

以上结果表明，在超静定结构中，温度应力是一个不容忽视的因素。在铁路钢轨接头处，以及混凝土路面中，通常都留有空隙；高温管道隔一段距离要设一个弯管，都为考虑温度的影响，调节因温度变化而产生的伸缩。如果忽视了温度变化的影响，将会导致破坏或妨碍结构物的正常工作。

§6-3扭转超静定问题

有些受扭杆件，其支反力偶矩或杆内的扭矩，仅靠静力学条件无法求解，即未知力的数目超过静力学平衡方程的数目，这类问题称为扭转超静定问题。

 【例2-4】 如图所示等直圆杆，已知 KN·m，试求杆两端的支反力偶矩。
【解】设两端约束扭转力偶为，
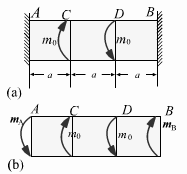（1）由静力平衡方程得

                 （a）
此题属于一次超静定。
  （2）由变形协调方程（可解除B端约束），用变形叠加法有
  （b）
（3）物理方程

，，  （c）
由式（c），（b）得

即

假设的力偶转向正确。

§6-4 简单超静定梁

1、  处理方法：变形协调方程、物理方程与静力学平衡方程相结合，求全部未知力。

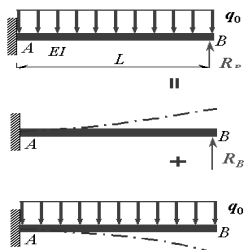
【例2-5】结构如图，求B点反力。

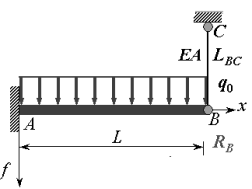【解】1） 建立静定基

2）几何方程—变形协调方程：

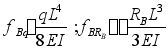
3） 物理方程——变形与力的关系

4）补充方程

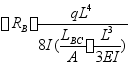
本章小结

1、              静定、超静定结构与超静定次数 

静定结构（或系统）：无多余联系的几何不变的承载结构系统，其支承反力及内力都可由静力学平衡方程求得，静定结构除了受力变形外，没有可运动的自由度。

超静定结构：在静定系统上增加多余约束，因而增加了多余约束未知力，用静力平衡方程不能确定其全部未知支承反力和内力的结构系统，称为超静定结构（或系统）。

超静定次数：超静定结构的所有未知支承反力和内力的总数与结构所能提供的独立的静力平衡方程数之差，即为此结构的超静定次数（或阶数）。

2、   静定系（静定基）与相当系统

解除静不定结构的某些约束后得到的静定结构，称为原静不定结构的基本静定系（又叫静定基）。在基本静定系上加上外载荷和多余约束力，这样的系统称为相当系统。

典型习题

典型习题6－1 设1、2、3三杆用铰链连接如图，已知：各杆长为：L1=L2、 L3 =L ；各杆面积为A1=A2=A、 A3 ；各杆弹性模量为：E1=E2=E、E3。外力沿铅垂方向，求各杆的内力。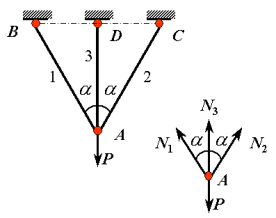解：1）平衡方程:

2） 几何方程——变形协调方程：

3）物理方程

由几何方程和物理方程得：

  联立以上各式：