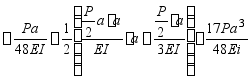第八部分 弯曲变形
8.1 预备知识
一、基本概念
1、积分法和叠加法求弯曲变形;
2、用变形比较法解超静定梁。
二、重点与难点
1、叠加法求弯曲变形;
2、用变形比较法解超静定梁。
三、解题方法要点
8.2 典型题解
一、计算题
一悬臂梁,梁上荷载如图所示,梁的弯曲刚度为EI,求自由端截面的转角和挠度。
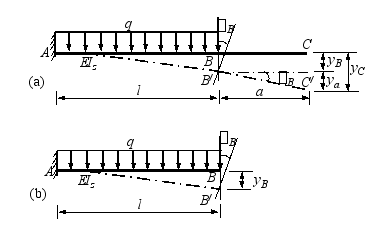
解:梁在荷载作用下的挠曲线如图8—7a中之虚线所示,其中B/C/段为直线,因之C、B两截面的转角相同,即
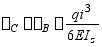
C截面的挠度可视为由现两部分组成,一为yB(即B截面的挠度,按图8—7b之简图求之),另一为由B截面转过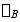 角而引起的C截面之位移
角而引起的C截面之位移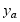 (B/C/段相当于刚体向下平移
(B/C/段相当于刚体向下平移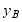 ,再绕B/点转过
,再绕B/点转过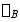 角)。因梁的变形很小,
角)。因梁的变形很小,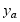 可用
可用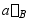 来表示。
来表示。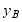 值可由查表得
值可由查表得
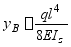
C截面的挠度为
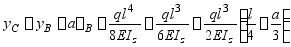
二、计算题
一悬臂梁,其弯曲刚度为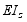 、梁上荷载如图所示,求C截面的挠度。
、梁上荷载如图所示,求C截面的挠度。
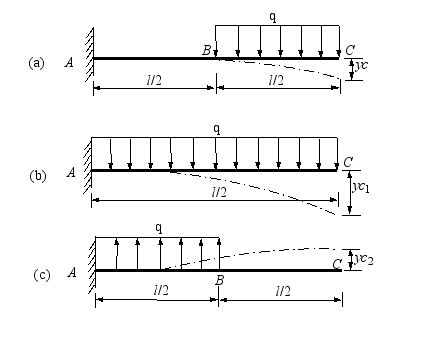
解:由于表中没有图所示情况的计算公式,但此题仍可用叠加法计算。图a的情况相当于图b、c两种情况的叠加。图b中C截面的找度为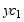 ,其值为
,其值为
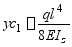
图c中C截面的挠度为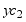 ,其值可按计算题一之方法,即
,其值可按计算题一之方法,即
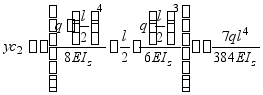
C截面的挠度则为
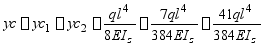
(此题是否还有其它叠加方法,读者可自行考虑之)。
三、计算题
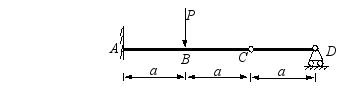
一外伸梁,梁上荷载如图所示。梁的弯曲刚度为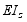 ,求C截面的挠度。
,求C截面的挠度。

解: 外伸梁在荷载作用下的挠曲线如图a中虚线所示,两支座处只产生转角而挠度等零。在计算C截面的挠度时,将梁的BC段可先看成B 端为固定端的悬臂梁(图c),此悬臂梁在均布荷载q的作用下,C截面的挠度为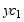 。但外伸梁上下班B截面并非固不动,而要产生转角
。但外伸梁上下班B截面并非固不动,而要产生转角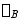 ,B截面转
,B截面转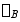 角使C截面也要产生向下的竖向位移(相当于刚体转动),该竖向位移用
角使C截面也要产生向下的竖向位移(相当于刚体转动),该竖向位移用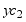 表示(图e)。将图c的
表示(图e)。将图c的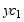 与图8—9e的
与图8—9e的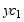 与图e中的
与图e中的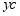 2相叠加,就是外伸梁上C截面的挠度
2相叠加,就是外伸梁上C截面的挠度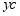 。即
。即
因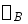 很小,
很小,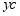 2可用
2可用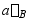 来表示。外伸梁上B截面的转角
来表示。外伸梁上B截面的转角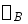 ,相当于图b所示荷载作用下简支梁上B截面的转角。因集中力
,相当于图b所示荷载作用下简支梁上B截面的转角。因集中力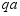 是作用在支座上,故不引起梁的变形,仅力矩
是作用在支座上,故不引起梁的变形,仅力矩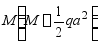 使梁变形。简支梁在
使梁变形。简支梁在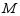 作用下B截面的转角可从表中查得为
作用下B截面的转角可从表中查得为 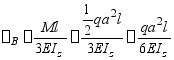
所以
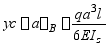
从表查得
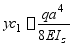
外伸梁上C截面的挠度则为
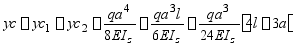
四、计算题
简支梁受三角形分布荷载作用,如图所示。
(1)试导出该梁的挠曲线方程;
(2)确定该梁的最大挠度。
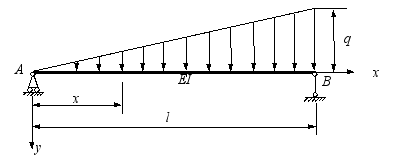
解:首先求支反力
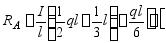
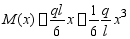
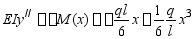
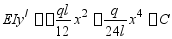
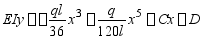
由边界条件:
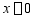 ,
, 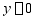
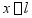 ,
, 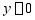
得D=0 ,C=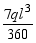
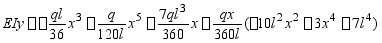
再求 。
。
令
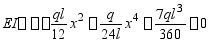
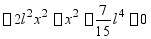
得
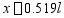
所以
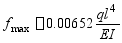
讨论 本题说明积分法求变形的具体作法,积分常数的确定以及最大挠度的确定;简支梁上,当截面转角为零时,挠度为最大值。本例y坐标正向向下,挠曲线近似微分方程改变符号。
五、计算题
抗弯刚度为EI的等直梁,其左端为一块滑动约束,并承受集中力P,如图。试求梁的挠曲线方程及滑块A的铅垂位移,梁跨度为 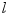 。
。
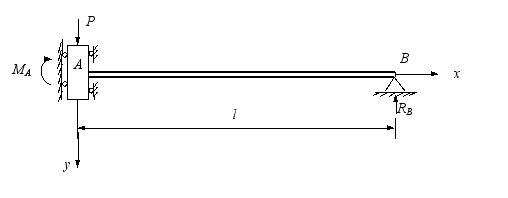
解:
求出梁在两端的支反力 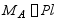 ,
, 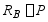
弯矩方程式
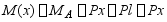
挠曲线微分方程为
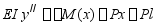
积分得

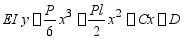
积分常数C、D由边界条件确定:
由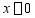 时,
时,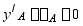 ,得
,得
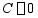
由 时,
时,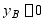 ,即
,即
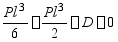

于是得挠曲线方程为:

滑块A的铅垂位移
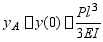
六、计算题
在图所示坐标系中,已知等直梁的挠曲线方程式为
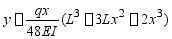
试求:
(1)最大弯矩最大剪力;
(2)梁两端(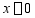 及
及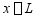 )的约束情况;
)的约束情况;
(3)梁上承受载荷的情况。

解:由挠度、转角、弯矩、剪力和载荷集度之间的微分关系
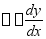 ,
, 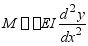 ,
,
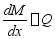 ,
, 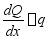
得
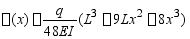
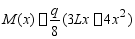
条件: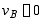 ,得补充方程:
,得补充方程:
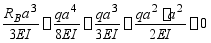
于是,得
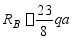
由静力平衡方程 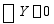
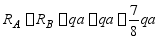
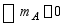
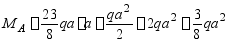
全部约束反力均已求得,可以直接画出该梁的剪力图和弯矩图。
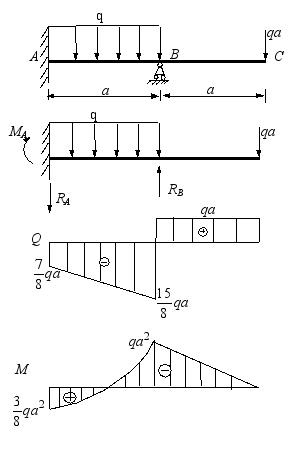
八、计算题
两悬臂梁AB和CD通过CB杆连接,两梁的截面刚度均为EI,杆的截面刚度为EF,试求CB杆所受的内力,并画出梁AB和CD的弯矩图。

解:一次静不定,显然,AB梁B点挠度与CD梁C点挠度之差等于BC杆的伸长量,即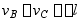
其中
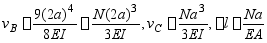
代入(a)式,解出


九、计算题
如图所示结构各杆EI相同。求E截面的铅垂位移(不计轴力和剪力对变形的影响)。

解:设B点的铅垂位移为 B,则E点因B点的铅垂位移而产生的铅垂位移为
B,则E点因B点的铅垂位移而产生的铅垂位移为 B/2,同时AB梁的弯曲使得E点产生挠度
B/2,同时AB梁的弯曲使得E点产生挠度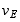 故E截面的铅垂位移为
故E截面的铅垂位移为
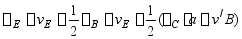
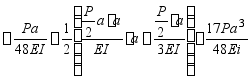
8.3 练习题
一、概念题
1、是非判断题
试判断下列论述是否正确,正确的在括号内打“√”,错误的打“╳”。
(1) 梁上弯矩最大的截面,挠度也最大,弯矩为零的截面,转角为零。( ╳ )
(2) 两根几何尺寸、支承条件完全相同的静定梁,只要所受荷载相同,则两梁所对应的截面的挠度及转角相同,而与梁的材料是否相同无关。 ( ╳ )
(3) 悬臂梁受力如图所示,若A点上作用的集中力P 在AB段上作等效平移,则A截面的转角及挠度都不变。 ( √ )
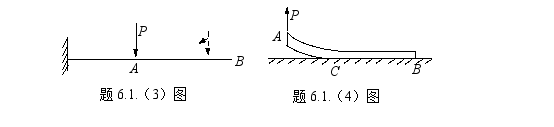
(4) 图示均质等直杆(总重量为W),放置在水平刚性平面上,若A端有一集中力P作用使AC部分被提起,CB部分仍与刚性平面贴合,则在截面C上的剪力和弯矩均为零。
( ╳ )
(5) 等截面直梁在弯曲变形时,挠曲线的曲率最大值发生在转角等于零的截面处。
( ╳ )
(6) 两简支梁的抗弯刚度EI及跨2a均相同,受力如图所示,则两梁跨中截面C的挠度不等而转角是相等的。 ( √ )
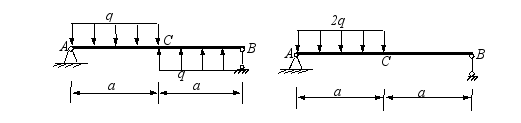
(7) 一铸铁简支梁,在均布截荷作用下,当其横截面相同且分别按图示两种情况放置时,梁同一截面的应力及变形均相同。 ( ╳ )

(8) 平面弯曲梁的挠曲线必定是一条与外力作用面重合或平行的平面曲线。 ( √ )
(9) 由于挠曲线的曲率与弯矩成正比,因此横截面的挠度和转角也与截面上的弯矩成正比。 ( ╳ )
(10) 只要满足线弹性条件(力与变形关系服从虎克定律),就可以应用挠曲线的近似微分方程 ( ╳ )
(11) 若两梁的抗弯刚度相同,弯矩方程相同,则两梁的挠曲线形状完全相同。
( √ )
(12) 梁的挠曲线方程随弯矩方程的分段而分段,只要梁不具有中间铰,则梁的挠曲线仍然是一条光滑、连续的曲线。 ( √ )
2、填空题
(1) 图示简支梁(a)、(b)受均布载荷作用,已知两梁的EI相等则(b)梁的最大挠度应为(a)梁的最大 16 倍。

(2)用积分法求图示梁变形法时,
边界条件为 ;
;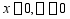 ;
;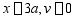
连续条件为 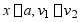 ;
;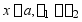 ;
;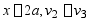
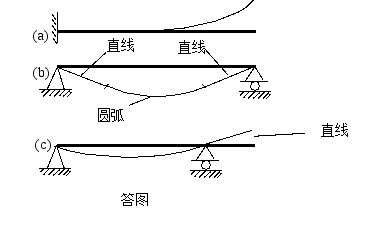
(3) 画出(a)、(b)、(c)三种梁的挠曲线大致形状。

答:
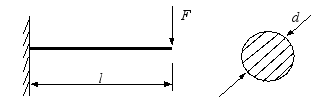
(4) 如图所示的圆截面悬臂梁,受集中力作用。(a)当梁的直径减少一倍而其他条件不变时,其最大弯曲正应力是原来的( 8 )倍,其最大挠度是原来的( 16 )倍;
(b)若梁的长度增大一倍,其他条件不变,则其最大弯曲正应力是原来的( 2 )倍,
最大挠度是原来的( 8 )倍。
(5) 如图所示的外伸梁,已知B截面转角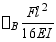 ,则C截面的挠度yc=(
,则C截面的挠度yc=(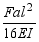 )。
)。

(6) 如图所示两梁的横截面大小形状均相同,跨度为l则两人的内力图( 相同 ),两梁的最大正应力( 相同 ),两梁的变形( 不同 )。(填“相同”或“不同”)

(7) 如图所示的简支梁,EI已知,则中性层在A处的曲率半每径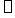 =(
=( 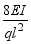 )
)
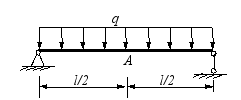
(8) 如图所示的圆截面外伸梁,直径d=7.5cm,F=10kN,材料的弹性模量E=200GPa,则AB段变形后的曲率半径为( 77.7m ),梁跨度中点C的挠度yc=( 3.6m )
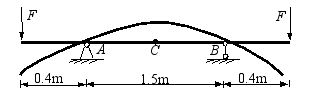
(9) 如图所示受均布载荷q作用的超静定梁,当跨度l增加一倍而其他条件不变时,跨
长中点C的挠度是原来的( 16 )倍。
3、选择题
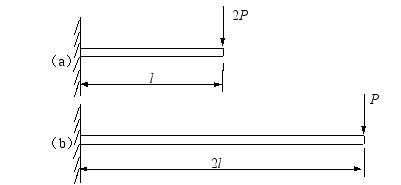
(1) 图示两梁的材料和截面相同,则两梁的最大挠度之比 ∶
∶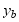 =( B )。
=( B )。
A 1 B 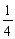 ;
;
C 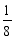 D
D 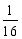
(2)图示结构的变形谐调条件为:
A 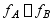 B
B 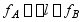
C  D
D 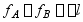 。
。
正确答案是 D 。

(3) 等截面直梁在弯曲变形时,挠曲线的曲率最大发生在( D )处。
A 挠度最大 B 转角最大
C 剪力最大 D 弯矩最大
(4) 应用叠加原理求梁横截面的挠度、转角时,需要满足的条件是( C )。
A 梁必须是等截面的 B 梁必须是静定的
C 变形必须是小变形; D 梁的弯曲必须是平面弯曲
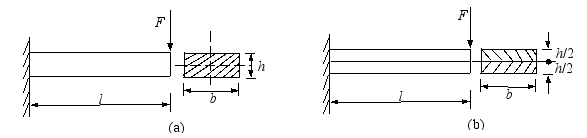
(5) 比较图示两梁强度和刚度,其中(b)梁由两根高为0.5h、宽度仍为b的矩形截面梁叠合而成,且相互间摩擦不计,则有( D )
A 强度相同,刚度不同 B 强度不同,刚度相同
C 强度和刚度均相同 D 强度和刚度均不相同
(6) 如图所示的两简支梁,一根为钢、一根为铜。已知它们的抗弯刚度相同,在相同的F力作用下,二者的( B )不同。
A 支反力 B 最大正应力
C 最大挠度 D 最大转角
(7) 如图所示的悬臂梁,为减少最大挠度,则下列方案中最佳方案是( B )
A 梁长改为l/2,惯性矩改为I/8 B 梁长改为3l4,惯性矩改为I/2
C 梁长改为5l/4,惯性矩改为3I/2 D 梁长改为3l/2,惯性矩改为I/4
二、计算题
1、 试对图示各梁列出确定积分常数的边界条件,抗弯刚度EI已知。
解答:(a) 边界条件: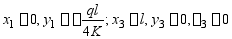
连续条件: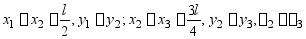
(b) 边界条件:
连续条件: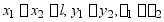

2、 用积分法计算图示梁的变形时,需分段建立方程?并写出其位移边界条件。

解答:应分三段,边界条件为:
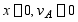
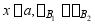 ;
;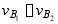
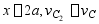
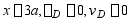
3、 试用叠加法求图示梁A截面的挠度及B截面的转角,EI为已知常量。
解答: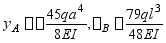

4、 试求图示各梁C截面的挠度,EI为常量。
解答:(a)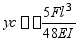 ; (b)
; (b)
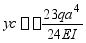
 5、 如图所示的简支梁由两根据地2a槽钢组成,E=200GPa,l=4m,q=10kN/m,
5、 如图所示的简支梁由两根据地2a槽钢组成,E=200GPa,l=4m,q=10kN/m,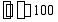 MPa,许用挠度
MPa,许用挠度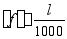 ,试校核其强度和刚度(考虑梁自重的影响)。
,试校核其强度和刚度(考虑梁自重的影响)。
答:
6、 如图所示的悬臂梁由此及彼2b工字钢制成,l=2m,E=200GPa, =120MPa,许用挠度
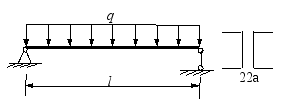
=120MPa,许用挠度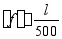 ,试确定许可均布荷载集度。
,试确定许可均布荷载集度。

答:5.08kN/m

![]()
![]() 角而引起的C截面之位移
角而引起的C截面之位移![]() (B/C/段相当于刚体向下平移
(B/C/段相当于刚体向下平移![]() ,再绕B/点转过
,再绕B/点转过![]() 角)。因梁的变形很小,
角)。因梁的变形很小,![]() 可用
可用![]() 来表示。
来表示。![]() 值可由查表得
值可由查表得![]()
![]()
![]() 、梁上荷载如图所示,求C截面的挠度。
、梁上荷载如图所示,求C截面的挠度。
![]() ,其值为
,其值为 ![]()
![]() ,其值可按计算题一之方法,即
,其值可按计算题一之方法,即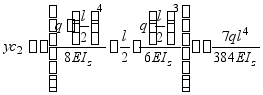
![]()
![]() ,求C截面的挠度。
,求C截面的挠度。
![]() 。但外伸梁上下班B截面并非固不动,而要产生转角
。但外伸梁上下班B截面并非固不动,而要产生转角![]() ,B截面转
,B截面转![]() 角使C截面也要产生向下的竖向位移(相当于刚体转动),该竖向位移用
角使C截面也要产生向下的竖向位移(相当于刚体转动),该竖向位移用![]() 表示(图e)。将图c的
表示(图e)。将图c的![]() 与图8—9e的
与图8—9e的![]() 与图e中的
与图e中的![]() 2相叠加,就是外伸梁上C截面的挠度
2相叠加,就是外伸梁上C截面的挠度![]() 。即
。即![]()
![]() 很小,
很小,![]() 2可用
2可用![]() 来表示。外伸梁上B截面的转角
来表示。外伸梁上B截面的转角![]() ,相当于图b所示荷载作用下简支梁上B截面的转角。因集中力
,相当于图b所示荷载作用下简支梁上B截面的转角。因集中力![]() 是作用在支座上,故不引起梁的变形,仅力矩
是作用在支座上,故不引起梁的变形,仅力矩![]() 使梁变形。简支梁在
使梁变形。简支梁在![]() 作用下B截面的转角可从表中查得为
作用下B截面的转角可从表中查得为 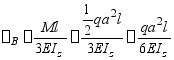
![]()
![]()
![]()