第四章 弯曲应力
§4-1 引言
杆件在横向力或弯矩作用下会发生弯曲变形,以弯曲变形为主的杆件常称作梁。轴线为直线的梁称为直梁,轴线为曲线的梁称为曲梁。当梁具有通过其轴线的纵向对称面、且作用于梁上的外力都在该对称面内时,变形后梁的轴线仍将是位于该对称面内的一条曲线,这种情况称作平面弯曲。这里主要介绍发生平面
弯曲的梁。
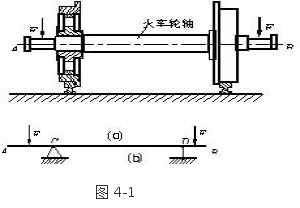
例如图(a)所示火车轮轴的计算简图,即分别如图(b)所示.
-、梁的计算简图
为了便于分析计算,应进行必要的简化,抽象出计算简图。
1.构件本身的简化 通常取梁的轴线代替梁。
2.载荷简化![]()
作用于梁上的载荷(包括支座反力)可简化为三种类型:
集中力、集中力偶和分布载荷。
3.梁的形式
(1) 简支梁
![]()
(2) 悬臂梁
![]()
(2) 外伸梁
![]()
静定梁:由静力学方程可求出支反力,如上述三种基本形式的静定梁。
超静定梁:由静力学方程不可求出支反力或不能求出全部支反力。.
§4-2梁的内力——剪力和弯矩
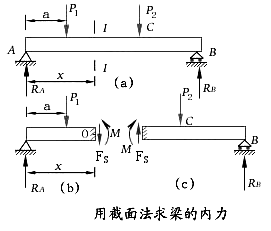
如图a所示的简支梁,其两端的支座反力![]() 、
、![]() 可由梁的静力平衡方程求得。用假想截面将梁分为两部分,并以左段为研究对象图b,由于梁的整体处于平衡状态,因此其各个部分也应处于平衡状态。据此,截面I―I上将产生内力,这些内力将与外力
可由梁的静力平衡方程求得。用假想截面将梁分为两部分,并以左段为研究对象图b,由于梁的整体处于平衡状态,因此其各个部分也应处于平衡状态。据此,截面I―I上将产生内力,这些内力将与外力![]() 、
、![]() ,在梁的左段构成平衡力系。
,在梁的左段构成平衡力系。
由平衡方程![]() ,则
,则
![]()
![]()
![]() 这一与横截面相切的内力
这一与横截面相切的内力![]() 称为横截面I―I上的剪力,它是与横截面相切的分布内力系的合力。
称为横截面I―I上的剪力,它是与横截面相切的分布内力系的合力。
根据平衡条件,若把左段上的所有外力和内力对截面I―I的形心![]() 取矩,其力矩总和应为零,即
取矩,其力矩总和应为零,即![]() ,则
,则
![]()
![]()
 这一内力偶矩
这一内力偶矩![]() 称为横截面I―I上的弯矩。它是与横截面垂直的分布内力系的合力偶矩。剪力和弯矩均为梁横截面上的内力,它们可以通过梁的局部平衡来确定。
称为横截面I―I上的弯矩。它是与横截面垂直的分布内力系的合力偶矩。剪力和弯矩均为梁横截面上的内力,它们可以通过梁的局部平衡来确定。
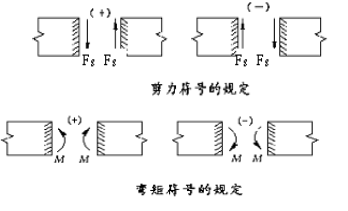
剪力、弯矩的正负号规定:使梁产生顺时针转动的剪力规定为正,反之为负,如图所示;使梁的下部
产生拉伸而上部产生压缩的弯矩规定为正,反之为负。
§4-3剪力、弯矩方程与剪力、弯矩图
一般情况下,在梁的不同横截面或不同梁段内,剪力与弯矩一般均不相同,即剪力与弯矩沿梁轴变化。
为了描写剪力与弯矩沿梁轴的变化情况,沿梁轴选取坐标x表示横截面的位置,并建立剪力、弯矩与坐标x间的解析关系式,即
![]()
![]()
上述关系式分别称为剪力方程与弯矩方程。
表示剪力与弯矩沿梁轴变化情况的另一重要方法为图示法.作图时,以x为横坐标轴,以剪力![]() 或弯矩M为纵坐标轴,分别绘制剪力与弯矩沿梁轴变化情况的曲线,上述曲线分别称为剪力图或弯矩图。
或弯矩M为纵坐标轴,分别绘制剪力与弯矩沿梁轴变化情况的曲线,上述曲线分别称为剪力图或弯矩图。
研究剪力与变矩沿梁轴的变化情况,对于解决梁的强度与刚度问题都是必不可少的.因此,剪力、弯矩方程与剪力、弯矩图是分析弯曲问题的重要基础。
例: 图a)所示简支梁,受集中力F作用,试写出梁的剪力方程和弯矩方程,并作剪力图与弯矩图。
解:1.求支反力
![]()
![]()
2.分段列剪力方程和弯矩方程。
因为C截面作用一集中力F,集中力两侧梁的内力方程不同,需要分别写出。
AC段,由分离体图b)的平衡方程,得到内力方程如下
![]()
 (0<
(0<![]() <
<![]() ) (a)
) (a)
![]() (0≤
(0≤![]() ≤
≤![]() ) (b)
) (b)
CB段,由分离体图c)的平衡方程,得到该段的内力方程如下
![]()
![]()
(c)
![]() (
(![]() ≤
≤![]() ≤
≤![]() ) (d)
) (d)
3.作剪力图与弯矩图
根据式(a)、(c)作出梁的剪力图如图d)所示;由式(b)、(d)作出梁的弯矩图如图e)所示。由图可见最大剪力发出生AC段的各横截面上,最大弯矩发生在集中力所在的C截面。其值分别
![]() ,
, ![]()
由剪力图还可看出,在集中力作用截面的两侧剪力值有一大小为F的突变。
§4-4 剪力、弯矩与载荷集度间的微分关系
本节研究载荷集度、剪力、弯矩三者的关系,及其在绘制剪力、弯矩图中的应用。
微段的平衡:
坐标系![]() 向左为正,载荷q(x),向上为正。
向左为正,载荷q(x),向上为正。
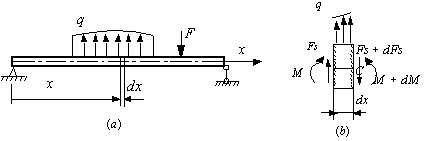
一、微(积)分关系
![]()
![]()
![]()
![]()
![]()
略去二阶微量,得
![]()
![]()
上述关系式表明:剪力图某点处的切线斜率,等于相应截面处的载荷集度;弯矩图某点处的切线斜率,等于相应截面的剪力;而弯矩图某点处的二阶导数,则等于相应截面处的载荷集度.
从数学上看,剪力、弯矩图就是函数的图象,因此可以利用函数的各种性质,包括微分和积分性质,总结出画剪力弯矩图的快捷方法。
几何意义(用来绘制剪力弯矩图)
正向规定:![]() 轴→,P,q
轴→,P,q![]() (由剪力、弯矩方程绘图时,不必加此限制。由微积分关系画图, 如正向规定不同,某些量会改变符号)
(由剪力、弯矩方程绘图时,不必加此限制。由微积分关系画图, 如正向规定不同,某些量会改变符号)
![]() 图:斜率=q,q=常数:直线
图:斜率=q,q=常数:直线![]()
P点跳,(P上指,![]() 图上跳)
图上跳)
(任意截面)![]() 图左边面积+集中力(含支反力)
图左边面积+集中力(含支反力)
![]() 图:斜率=
图:斜率=![]()
![]() 点跳(
点跳(![]() 顺时针,
顺时针,![]() 上跳)
上跳)
![]()
![]() ,
,![]() 极值(或拐点)
极值(或拐点)
凹凸性:![]()
(任意截面)![]() 图左边面积+集中力偶(含支反力偶)
图左边面积+集中力偶(含支反力偶)
例 图a)示简支梁承受均布载荷作用,载荷集度为q,梁的长度为l,试作梁的![]() 、Mz图。
、Mz图。
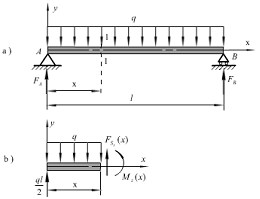 解:1.求支反力
解:1.求支反力
![]()
2.列内力方程
很显然由于载荷无突变,梁的剪力和弯矩各用一个函数表达式来描述。由分离体图b)的平衡得到内力方程如下
![]() (0<x<l) (a)
(0<x<l) (a)
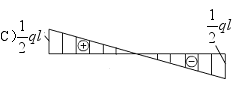
![]() (0≤x≤l) (b)
(0≤x≤l) (b)
3.作![]() 、Mz图
、Mz图
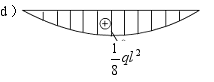 由式(a)看出,剪力方程是线性的,求出梁两个端截面的剪力值即可作
由式(a)看出,剪力方程是线性的,求出梁两个端截面的剪力值即可作![]() 图如图c)所示。由式(b)可见,弯矩图为一抛物线。将式(b)对x导数,并令其为零
图如图c)所示。由式(b)可见,弯矩图为一抛物线。将式(b)对x导数,并令其为零
![]() (c)
(c)
由此求得弯矩有极值的截面位置为x =l/2,将其代入式(b),得弯矩的极大值Mzmax=ql2/8
作出的弯矩图如d)图所示。
§4-5 弯曲正应力
一. 概述
一般情况下,梁横截面上既有弯矩M,又有剪力Q.
只有法向内力元素dN=![]() dA,才能组成M.
dA,才能组成M.
只有切向内力元素dQ=![]() dA,才能组成Q.
dA,才能组成Q.
本章讨论平面弯曲下梁横截面上的应力计算,先从纯弯曲推导,后推广至横力弯曲的一般情况。
二. 梁横截面上正应力
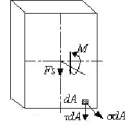 从三个方面来考察。
从三个方面来考察。
1.几何方面
发生纯弯曲(pure bending)时,剪力影响微弱,可忽略。由变形现象观察可知,变形符合平面假设。
![]()
![]()
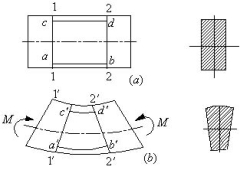
变形现象:(1)横截面仍是平面。
(2)直线变曲线,有伸有缩。
(3)横截面与轴线仍正交。
a-b线伸长,c-d线缩短。其都为同心圆弧。若变形前a-b,c-d线至轴线的距离一样,则其伸长、缩短程度一样。沿梁高,变形协调变化。从伸到缩,总有一层不伸不缩层,称为中性层。中性层与轴线重合。
中性轴(neutral axis)----中性层与横截面之交线。
找任意位置处与轴线平行的线段的应变。如梁微段长dx的变形后的o-o线。因为应力等于弹性模量乘以线应变,故先找线应变。
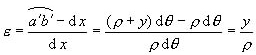
距中性层等远处纤维伸长、缩短未变,与z轴方向位置无关。中性层曲率半径,故![]() 代入应变式后,
代入应变式后,![]()
2.物理方面
无因纯弯曲而引起的纤维挤压。E相等,拉、压均有
![]() ,正应力与所求点到中性轴距离成正比。
,正应力与所求点到中性轴距离成正比。
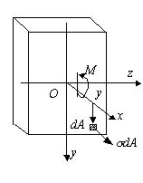
3.静力学方面
![]() 只可能组成三个内力分量。
只可能组成三个内力分量。
![]()
由求内力的截面法知,内力只有M.所以
![]()
将![]() 代入上三式:
代入上三式:
![]() ,说明z轴须过形心。
,说明z轴须过形心。
![]() ,y是对称轴。
,y是对称轴。
![]() ,Iz(moment of inertia)为截面对z轴的惯性矩。所以
,Iz(moment of inertia)为截面对z轴的惯性矩。所以![]() ,EIz为抗弯刚度。
,EIz为抗弯刚度。
将上式代入正应力表达式:![]() ,此即弯曲正应力公式。
,此即弯曲正应力公式。
其中M----弯矩,y----所求点距中性轴距离,Iz----惯性矩。
正应力的正负由y决定。基本单位:Pa.
截面上最大正应力:![]() ,令
,令![]() ,则
,则
![]()
其中Wz----抗弯截面模量。
横力弯曲时,除了内力弯矩外,还有内力剪力,但由于剪力一般情况下引起的变形很小,基本不影响以上推导,故上式推广到横力弯曲情况。
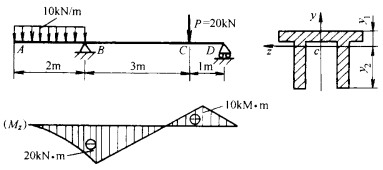
例 图示一用铸铁制成的Ⅱ字形截面梁。已知:截面图形对形心轴的惯性矩Iz=4.5×107mm4,y1=50mm,y2 = 140mm;材料许用拉应力及许用压应力分别为[�������� t] = 30MPa,[�������� c] = 140MPa。试按正应力强度条件校核强度。
解:画弯矩图,由图可见B、C两截面弯矩符号不同。注意到截面上的中性轴为非对称轴,且材料的拉、压许用应力数值不等,故B、C两截面均可能为危险截面。
B截面
![]()
![]()
C截面 ![]()
最大拉应力在C截面,最大压应力在B截面。且 ![]() ,而
,而 ![]() 虽略大于[��������
虽略大于[��������![]() ],但未超过5%,故可认为弯曲正应力基本
],但未超过5%,故可认为弯曲正应力基本
上能满足强度要求。
§4-6 横截面上的弯曲剪应力
梁受横弯曲时,虽然横截面上既有正应力![]() ,又有剪应力
,又有剪应力![]() 。但一般情况下,剪应力对梁的强度和变形的影响属于次要因素,因此对由剪力引起的剪应力,而是在正应力公式仍然适用的基础上,假定剪应力在横截面上的分布规律,然后根据平衡条件导出剪应力的计算公式。
。但一般情况下,剪应力对梁的强度和变形的影响属于次要因素,因此对由剪力引起的剪应力,而是在正应力公式仍然适用的基础上,假定剪应力在横截面上的分布规律,然后根据平衡条件导出剪应力的计算公式。
1 矩形截面梁的弯曲切应力
图示矩形截面梁,在纵向对称面内承受任意载荷作用。设横截面的高度为![]() ,
,
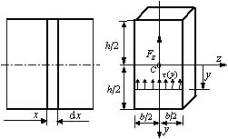
宽度为b ,现在研究弯曲切应力的分布规律。
对弯曲切应力分布作如下假设:横截面上各点
处的切应力,均平行于剪力或截面侧边,并沿截
面宽度均匀分布。
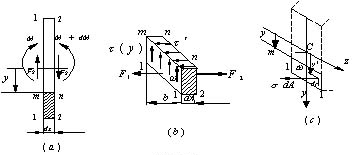
现在研究弯曲切应力沿截面高度的变化规律。
现欲求距中性轴z为y的横线![]() 处的剪应力
处的剪应力![]() 。过
。过![]() 用平行于中性层的纵截面自dx微段中截出一微块(b)。根据剪应力成对定理,微块的纵截面上存在均匀分布的剪应力
用平行于中性层的纵截面自dx微段中截出一微块(b)。根据剪应力成对定理,微块的纵截面上存在均匀分布的剪应力![]() 。微块左右侧面上正应力的合力分别为
。微块左右侧面上正应力的合力分别为![]() 和
和![]() ,其中
,其中
![]() (a)
(a)
![]() (b)
(b)
式中,![]() 为微块的侧面面积,
为微块的侧面面积,![]() 为面积
为面积![]() 中距中性轴为
中距中性轴为![]() 处的正应力,
处的正应力,![]() 。
。
由微块沿x方向的平衡条件![]() ,得
,得
![]() (c)
(c)
将式(a)和式(b)代入式(c),得
![]()
故 ![]()
因![]() ,故求得横截面上距中性轴为y处横线上各点的剪应力
,故求得横截面上距中性轴为y处横线上各点的剪应力![]() 为
为
![]() 式中:
式中:![]() 为整个工字形截面对中性轴
为整个工字形截面对中性轴![]() 的惯性矩,而
的惯性矩,而![]() 则代表 处横线一侧的部分截面(面积为A)对
则代表 处横线一侧的部分截面(面积为A)对![]() 轴的静矩(图5-28),其值为:
轴的静矩(图5-28),其值为:
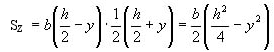
![]()
将上式及![]() 代入式(5-11),于是得
代入式(5-11),于是得
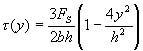
由此可见:矩形截面梁的弯曲切应力沿截高度呈抛物线分布(图5-28b);在截面的上、下边缘![]() ,切应力
,切应力![]() ;在中性轴处
;在中性轴处![]() ,切应力最大,其值为
,切应力最大,其值为
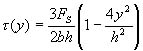
 2.圆形截面梁的弯曲切应力
2.圆形截面梁的弯曲切应力
在圆形截面上,任一平行于中性轴的横线aa![]() 两端处,剪应力的方向必切于圆周,并相交于y轴上的c点。因此,横线上各点剪应力方向是变化的。但在中性轴上各点剪应力的方向皆平行于剪力Q,设为均匀分布,其值为最大。由式
两端处,剪应力的方向必切于圆周,并相交于y轴上的c点。因此,横线上各点剪应力方向是变化的。但在中性轴上各点剪应力的方向皆平行于剪力Q,设为均匀分布,其值为最大。由式
![]()
求得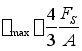
式中![]() ,即圆截面的最大剪应力为其平均剪应力的
,即圆截面的最大剪应力为其平均剪应力的![]() 倍。
倍。
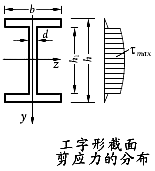 3.工字形截面梁的弯曲切应力
3.工字形截面梁的弯曲切应力
工字形截面梁由腹板和翼缘组成。式(6-3)的计算结果表明,在翼缘上剪应力很小,在腹板上剪应力沿腹板高度按抛物线规律变化,如图所示。最大剪应力在中性轴上,其值为
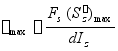
式中(S![]() )
)![]() 为中性轴一侧截面面积对中性轴的静矩。对于轧制的工字钢,式中的
为中性轴一侧截面面积对中性轴的静矩。对于轧制的工字钢,式中的![]() 可以从型钢表中查得。
可以从型钢表中查得。
计算结果表明,腹板承担的剪力约为(0.95~0.97)![]() ,因此也可用下式计算
,因此也可用下式计算![]()
![]() 的近似值
的近似值
![]()
式中h![]() 为腹板的高度,d为腹板的宽度。
为腹板的高度,d为腹板的宽度。
§4-6 梁的强度条件
一、弯曲正应力强度条件
最大弯曲正应力发生在横截面上离中性轴最远的各点处,而该处的切应力一般为零或很小,因而最大弯曲正应力作用点可看成是处于单向受力状态,所以,弯曲正应力强度条件为
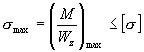
对于等截面直梁,上式变为
![]()
上式仅适用于许用拉应力[σt]与许用压应力[σc]相同的梁,如果二者不同,例如铸铁等脆性材料的许用压应力超过许用拉应力,则应按拉伸与压缩分别进行强度计算。
此式一般可进行三方面工作:
1.强度校核。![]() ,考核强度是否够。
,考核强度是否够。
2.设计截面。![]() ,按正应力强度,使梁的材料最省。
,按正应力强度,使梁的材料最省。
3.确定最大荷载。![]() ,按正应力强度,使物尽其用。
,按正应力强度,使物尽其用。
二、弯曲切应力强度条件
最大弯曲切应力通常发生在中性轴上各点处,而该处的弯曲正应力为零,因此,最大弯曲切应力作用点处于纯剪切状态,相应的强度条件则为
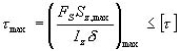
即要求梁内的最大弯曲切应力![]() 不超过材料在纯剪切时的许用切应力
不超过材料在纯剪切时的许用切应力![]() 。对于等截面直梁,上式变为
。对于等截面直梁,上式变为
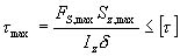
三、需要校核剪应力的几种特殊情况:
(1)梁的跨度较短,M 较小,而FS较大时,要校核剪应力。
(2)铆接或焊接的组合截面,其腹板的厚度与高度比小于型钢的相应比值时,要校核剪应力。
(3)各向异性材料(如木材)的抗剪能力较差,要校核剪应力。
§4-7提高弯曲强度的措施
提高弯曲强度的措施主要是从三方面考虑:采用梁的合理截面、减小最大弯矩和提高材料的力学性能。
梁的合理截面从两方面考虑:一是同一截面,二是全梁。
一、.梁的合理截面
梁的合理截面从两方面考虑:一是同一截面,二是全梁。为减轻自重,节约使用材料,根据梁截面应力分布情况,参照材料力学性能,弯矩一定时为梁选用合理截面。梁强度常由横截面正应力控制,弯矩一定,最大正应力与抗弯截面模量成反比,而W与高度平方成正比。面积不变时,材料重量不变。要使正应力小,只有尽可能地使抗弯截面模量大,那就最好增加其高度,使面积尽量分布在离中性轴较远的各点处。这样,惯性矩就大,Wz也跟着增大。此外,距中性轴最远处分别有最大拉应力和最大压应力。为了充分发挥材料的潜力,应尽量使材料沿整个截面同时达到相应的许用应力,这就是合理截面的出发点。
塑性材料梁,如钢梁,拉压许用应力相等,为满足使同时达到许用应力的要求,截面形状应使得中性轴为对称轴。脆性材料梁使用T形截面较合理。
措施:
使Wz增大,即增加梁高。
使截面同时达到许用应力。(塑、脆性材料不同,前者用对称性截面,后者用非对称截面)
二、采用变截面梁。
对于等截面梁,除![]() 所在截面的最大正应力达到材料的许用应力外,其余截面的应力均小于,甚至远小于许用应力。因此,为了节省材料,减轻结构的重量,可在弯矩较小处采用较小的截面,这种截面尺寸沿梁轴线变化的梁称为变截面梁。弯矩不定时,弯矩图指出弯矩沿梁轴线的变化,一般危险面只一处、或一段,这样,就未充分利用小弯矩处的材料。改进措施就是采用变截面梁。措施:
所在截面的最大正应力达到材料的许用应力外,其余截面的应力均小于,甚至远小于许用应力。因此,为了节省材料,减轻结构的重量,可在弯矩较小处采用较小的截面,这种截面尺寸沿梁轴线变化的梁称为变截面梁。弯矩不定时,弯矩图指出弯矩沿梁轴线的变化,一般危险面只一处、或一段,这样,就未充分利用小弯矩处的材料。改进措施就是采用变截面梁。措施:
因为![]() ,所以尽量使各截面应力相等。W(x)即为轴线自变量的函数。
,所以尽量使各截面应力相等。W(x)即为轴线自变量的函数。
若使变截面梁每个截面上的最大正应力都等于材料的许用应力,则这种梁称为等强度梁。考虑到加工的经济性及其他工艺要求,工程实际中只能作成近似的等强度梁,例如机械设备中的阶梯轴。
三.、减小最大弯矩
1).改变加载的位置或加载方式
首先,可以通过改变加载位置或加载方式达到减小最大弯矩的目的。如当集中力作用在简支梁跨度中间时,其最大弯矩为![]() ;当载荷的作用点移到梁的一侧,如距左侧
;当载荷的作用点移到梁的一侧,如距左侧![]() 处,则最大弯矩变为
处,则最大弯矩变为![]() ,是原最大弯矩的
,是原最大弯矩的![]() 倍。当载荷的位置不能改变时,可以把集中力分散成较小的力,或者改变成分布载荷,从而减小最大弯矩。例如利用副梁把作用于跨中的集中力分散为两个集中力,而使最大弯矩降低为
倍。当载荷的位置不能改变时,可以把集中力分散成较小的力,或者改变成分布载荷,从而减小最大弯矩。例如利用副梁把作用于跨中的集中力分散为两个集中力,而使最大弯矩降低为![]() 。利用副梁来达到分散载荷,减小最大弯矩是工程中经常采用的方法。
。利用副梁来达到分散载荷,减小最大弯矩是工程中经常采用的方法。
2)改变支座的位置
![]() 其次,可以通过改变支座的位置来减小最大弯矩。例如图(a)所示受均布载荷的简支梁,。
其次,可以通过改变支座的位置来减小最大弯矩。例如图(a)所示受均布载荷的简支梁,。
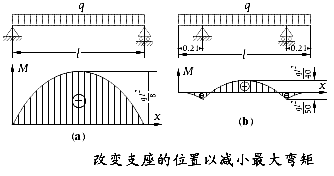
![]() 若将两端支座各向里移动
若将两端支座各向里移动![]() (图b),则最大弯矩减小为
(图b),则最大弯矩减小为
只及前者的1/5。
 例1 矩形(b´������h=0.12m´������0.18m)截面木梁如图,[]=7MPa,[t]=0. 9 M Pa,试求最大正应力和最大剪应力之比,并校核梁的强度。
例1 矩形(b´������h=0.12m´������0.18m)截面木梁如图,[]=7MPa,[t]=0. 9 M Pa,试求最大正应力和最大剪应力之比,并校核梁的强度。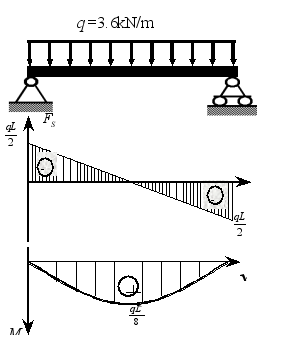

![]()
应力之比
 例3 T 字形截面的铸铁梁受力如图,铸铁的[sL]=30MPa,[sy]=60 MPa,其截面形心位于C点,y1=52mm, y2=88mm,Iz=763cm4 ,试校核此梁的强度。并说明T字梁怎样放置更合理?
例3 T 字形截面的铸铁梁受力如图,铸铁的[sL]=30MPa,[sy]=60 MPa,其截面形心位于C点,y1=52mm, y2=88mm,Iz=763cm4 ,试校核此梁的强度。并说明T字梁怎样放置更合理?
解:1.画弯矩图并求危险截面内力
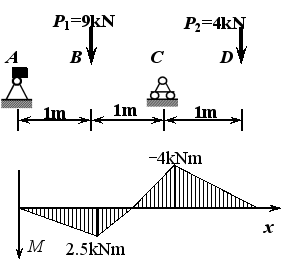
![]()
![]()
![]()
2.画危险截面应力分布图,找危险点
![]()
![]()
![]()
校核强度
T字头在上面合理![]()
![]()