第二章 轴向拉伸和压缩

§2-1轴向拉伸和压缩的概念

一、工程实例

 连杆、螺栓、桁架、房屋立柱、桥墩……等等。

二、特点

外力特点:外力合力作用线与轴线重合。

变形特点：沿杆轴伸长或缩短，同时横向尺寸缩小或增大。

轴向拉伸：杆的变形是轴向伸长，横向缩短  

轴向压缩：杆的变形是轴向缩短，横向变粗。 

§2-2 内力 · 截面法 · 轴力及轴力图 

一、内力的概念
内力：指由外力作用所引起的、物体内相邻部分之间分布内力系的合成（附加内力）。注意：材料力学中的内力，是指外力作用下而引起的内力的变化量，也就是“附加内力”，它与构件的强度、密度相关。

二、截面法 · 轴力

内力的计算是分析构件强度、刚度、稳定性等问题的基础。求内力的一般方法是截面法。

1. 截面法的基本步骤：

① 截开：在所求内力的截面处，假想地用截面将杆件一分为二。

②代替：任取一部分，其弃去部分对留下部分的作用，用作用在截开面上相应的内力（力或力偶）代替。

③平衡：对留下的部分建立平衡方程，根据其上的已知外力来计算杆在截开面上的未知内力（此时截开面
上的内力对所留部分而言是外力）。

3. 轴力——轴向拉压杆的内力，用N 表示。
4. 轴力的正负规定:

材料力学中轴力的符号是由杆件的变形决定，而不是由平衡坐标方程决定。习惯上将轴力N的正负号规定为：拉伸时，轴力N为正；压缩时，轴力N为负。

注意两个问题：

1）外力不能沿作用线移动。因为材料力学中研究的对象是变形体，不是刚体，力的可传性不成立。

2）截面不能切在外力作用点处，要离开或稍微离开作用点。依据为圣维南原理：作用在结构某一位置上的不同载荷，如果在静力学意义上是等效的，则在远离该位置处的应力差异甚微。

三、轴力图

以平行于杆轴线的坐标为x坐标，表示横截面的位置；以垂直于轴线的坐标FN为坐标，表示各横截面轴力FN的大小，画出的图形称为轴力图。

意义：①反映出轴力与截面位置变化关系，较直观；

②确定出最大轴力的数值及其所在横截面的位置，即确定危险截面位置，为强度计算提供依据。

习惯上，将正值的轴力画在上侧，负值的轴力画在下侧。

例2-1  求如图2-7所示杆件的内力，并作轴力图。

解：（1）计算各段内力

AC段：作截面1—1，取左段部分（图b）。由得

 kN   （拉力）

CD段：作截面2—2，取左段部分（图c），并假设方向如图所示。

由得

则

  kN  （压力）

的方向应与图中所示方向相反。

（2）绘轴力图

选截面位置为横坐标；相应截面上的轴力为纵坐标，根据适当比例，绘出图线。

由图2-7可知CB段的轴力值最大，即kN，所以CB段最危险。以平行于杆轴线的坐标为X坐标，表示横坐标的位置；以垂直于杆轴线的坐标FN为坐标，

§2-3  应力·拉（压）杆内的应力

一、应力的概念

问题提出： 

1. 内力大小不能衡量构件强度的大小。

2. 强度：①内力在截面分布集度应力；

         ②材料承受荷载的能力。 

1.  定义：由外力引起的内力集度。 

工程构件，大多数情形下，内力并非均匀分布，集度的定义不仅准确而且重要，因为“破坏”或“失效”往往从内力集度最大处开始。

2.  应力的表示： 

如图所示，在截面m—m上任一点K的周围取一微小面积ΔA，并设作用在该面积上的内力为ΔF，则ΔF与ΔA的比值，称为ΔA内的平均应力，并用p表示，即         

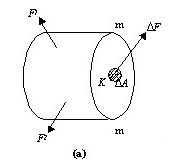
一般情况下，内力沿截面并非均匀分布，平均应力p之值及其方向将随所取面积ΔA的大小而异。为了更精确地描写内力的分布情况，应使ΔA趋于零，由此所得平均应力p的极限值，称为截面m—m上点K处的应力，并用表示,即：

显然，应力的方向即的极限方向。为了分析方便，通常将应力沿截面的法向与切向分解为两个分量（图b）。沿截面法向的应力分量称为正应力，并用表示；沿截面切向的应力分量称为切应力，并用τ表示。显然，

在我国法定计量单位中，力与面积的基本单位分别为N与m2，应力的单位为Pa（帕），其名称为“帕斯卡”（pascal），1Pa=1N/m2.。应力的常用单位为MPa2，其值为
　　　　　　　　　　　　　　　　　1Mpa=106 Pa　　　　　　　　　　　　　　

3.拉（压杆）横截面上的应力

1. 
   变形规律试验及平面假设 

变形前 

变形后

现象：横线仍为直线，且仍垂直于杆件轴线，只是间距增大，分别平移至图 与 位置.

平面假设：原为平面的横截面在变形后仍为平面。纵向纤维变形相同。 

根据上述现象，对杆内应力作如下假设：横截面上各点处仅存在正应力，并沿截面均匀分布.
　　设杆件横截面面积为A，轴力为FN，则根据上述假设可知，横截面上各点处的正应力均为

　　　　　　　　　　　（2－1）

或

式（2－1）已为试验所证实，适用于横截面为任意形状的等截面直杆.
由式（2－1）可知，正应力与轴力具有相同的正负符号，即拉应力为正，压应力为负

4.  公式的应用条件： 

直杆、杆的截面无突变、截面到载荷作用点有一定 的距离。 

5.  Saint-Venant原理： 

离开载荷作用处一定距离，应力分布与大小不受外载荷作用方式的影响。 

对于等截面直杆，由式（2-1）知最大正应力发生在最大轴力处，也就是最易破坏处。而对于变截面直杆，最大正应力的大小不但要考虑，同时还要考虑。

例  起吊三角架，如图2-10所示，已知AB杆由2根截面面积为cm2的角钢制成，kN，。求AB杆横截面上的应力。

解：（1）计算AB杆内力

取节点A为研究对象，由平衡条件，得

则

kN（拉力）

（2）计算

MPa

例  起吊钢索如图2-11所示，截面积分别为cm2，cm2，m，kN，N/cm3，试绘制轴力图，并求。

解：（1）计算轴力

AB段：取1—1截面

                               ①

BC段：取2—2截面

               ②

（2）绘轴力图

当时，kN    （拉力）

当时，kN    （拉力）

当时，kN    （拉力）

当时，kN    （拉力）

轴力图如图2-11b。

（3）应力计算

MPa   （拉应力）

MPa   （拉应力）

比较，的大小，得Mpa

4.拉（压）杆斜截面上的应力

以上研究了拉压杆横截面上的应力，为了更全面地了解杆内的应力情况，现在研究斜截面上的应力.
　　考虑如图所示拉压杆，利用截面法，沿任一斜截面m－m将杆切开，该截面的方位以其外法线On与x轴的夹角 表示.由前述分析可知，杆件横截面上的应力均匀分布，由此可以推断，斜截面m－m上的应力也均匀分布（图b），且其方向必与杆轴平行

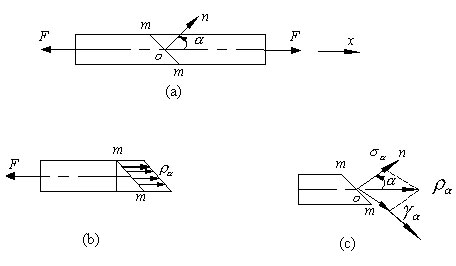
设杆件横截面的面积为Ａ，则根据上述分析，得杆左段的平衡方程为

由此得截面m-m上各点处的应力为

式中，，代表杆件横截面上的正应力

将应力沿截面法向与切向分解(图c)，得斜截面上的正应力与切应力分别为

可见，在拉压杆的任一斜截面上，不仅存在正应力，而且存在切应力，其大小则均随截面的方位角变化.
　　由式(2-2)可知，当时，正应力最大,其值为

即拉压杆的最大正应力发生在横截面上，其值为.
　　由式(2-3)可知，当α=45°时，切应力最大，其值为

即拉压力的最大切应力发生在与杆轴成45°的斜截面上，其值为 .
　　为便于应用上述公式，现对方位角与切应力的正负符号作如下规定：以x轴为始边，方位角α为逆时针转向者为正；将截面外法线沿顺时针方向旋转90°，与该方向同向的切应力为正.按此规定，如图所示之α与均为正.

补充：

1.一点的应力状态：过一点有无数的截面，这一点的各个截面上的应力情况，称为这点的应力状态。

2、单元体：①单元体—构件内的点的代表物，是包围被研究点的无限小的几何体，常用的是正六面体

②单元体的性质—a、平行面上，应力均布；b、平行面上，应力相等。

§2-4  拉（压）杆的变形·胡克定律

一、拉压杆的变形 

1、 
杆的纵向总变形：

3、  线应变：单位长度的线变形。

3、平均线应变： 

4、x点处的纵向线应变：

5、杆的横向变形：

6、x点处的横向线应变：

二、拉压杆的胡克定律

弹性定律是材料力学等固体力学一个非常重要的基础。一般认为它是由英国科学家胡克(1635一1703)首先提出来的，所以通常叫做胡克定律。 

1、 

等内力拉压杆的胡克定律

“EA”称为杆的抗拉压刚度。

2、 

单向应力状态下的胡克定律　

3、  泊松比（或横向变形系数）

4、

4、例 设横梁ABCD为刚梁，横截面面积为 76.36mm² 的钢索绕过无摩擦的定滑轮。设 P=20kN，试求刚索的应力和 C点的垂直位移。设刚索的 E =177GPa。 

解： 方法1：小变形放大图法 

1）求钢索内力：以ABCD为对象 

2) 钢索的应力和伸长分别为：

3）变形图如左图 ,C点的垂直位移为：  

§1－5 拉（压）杆内的应变能

变形能：弹性体在外力作用下，因变形而储存的能量称为变形能。

          （1）

下面以图2-27来讨论轴向拉伸或压缩的变形能。对轴向拉压（杆），拉力P作功为

        （2）

所以，由胡克定律，得

即轴向拉（压）杆的变形能为

比能（比密度）：单位体积的变形能，即

由胡克定律，则得

单位为焦/米3，J/m3。

例 设横梁ABCD为刚梁，横截面面积为 76.36mm² 的钢索绕过无摩擦的定滑轮。设 P=20kN，试求刚索的应力和 C点的垂直位移。设刚索的 E =177GPa。 

解：方法2：能量法：利用应变能的概念解决与结构物或构件的弹性变形有关的问题，这种方法称为能量法。（外力功等于变形能）  

（1）求钢索内力：以ABD为对象： 

（2） 钢索的应力为：

（3） C点位移为： 

§2-6  材料拉伸和压缩时的力学性能

一、  材料的力学性能与基本实验

    材料在外力作用下所表现出的变形和破坏方面的特性，称为材料的力学性能。材料的力学性能通常都是通过实验来认识的，最基本的实验是材料的轴向拉伸和压缩实验。常温、静载下的轴向拉伸试验是材料力学中最基本、应用最广泛的试验。通过拉伸试验，可以较全面地测定材料的力学性能指标，如弹性、塑性、强度、断裂等。这些性能指标对材料力学的分析计算、工程设计、选择材料和新材料开发有极其重要的作用，特别对建立复杂应力状态下材料的失效准则提供最基本的依据。由于有些材料在拉伸和压缩时所表现的力学性能并不相同，因而必须通过另一基本实验，轴向压缩实验来了解材料压缩时的力学性能。

    试验时首先要把待测试的材料加工成试件，试件的形状、加工精度和试验条件等都有具体的国家标准或部颁标准规定。例如，国家标准GB6397-86《金属拉伸试验试样》中规定拉伸试件截面可采用圆形和矩形（见图1），并分别具有长短两种规格。圆截面长试件其工作段长度（也称标距），短试件l 0 = 5d 0（图1a）；矩形截面长试件l0 = 11.3，短试件l 0 = 5.65，A 0为横截面面积（图1b）。金属材料的压缩实验，一般采用短圆柱形试件，其高度为直径的1.5~3倍（图1c）。除此之外，还规定了试验条件、试验内容及方法等。

二、  轴向拉伸和压缩实验 

1.  低碳钢的拉伸实验

    将试件装卡在材料试验机上进行常温、静载拉伸试验，直到把试件拉断，试验机的绘图装置会把试件所受的拉力F和试件的伸长量l之间的关系自动记录下来，绘出一条F - l曲线，称为拉伸图。研究拉伸图，并测定材料力学性能的各项指标。

   1）低碳钢的拉伸图

    图为低碳钢试件的拉伸图。由图可见，在拉伸试验过程中，低碳钢试件工作段的伸长量l与试件所受拉力F之间的关系，大致可分为以下四个阶段。

    第 Ⅰ 阶段  试件受力以后，长度增加，产生变形，这时如将外力卸去，试件工作段的变形可以消失，恢复原状，变形为弹性变形，因此，称第 Ⅰ 阶段为弹性变形阶段。低碳钢试件在弹性变形阶段的大部分范围内，外力与变形之间成正比，拉伸图呈一直线。

    第 Ⅱ 阶段  弹性变形阶段以后，试件的伸长显著增加，但外力却滞留在很小的范围内上下波动。这时低碳钢似乎是失去了对变形的抵抗能力，外力不需增加，变形却继续增大，这种现象称为屈服或流动。因此，第 Ⅱ 阶段称为屈服阶段或流动阶段。屈服阶段中拉力波动的最低值称为屈服载荷，用Fs表示。在屈服阶段中，试件的表面上呈现出与轴线大致成45的条纹线，这种条纹线是因材料沿最大切应力面滑移而形成的，通常称为滑移线。

    第 Ⅲ 阶段  过了屈服阶段以后，继续增加变形，需要加大外力，试件对变形的抵抗能力又获得增强。因此，第 Ⅲ 阶段称为强化阶段。强化阶段中，力与变形之间不再成正比，呈现着非线性的关系。

超过弹性阶段以后，若将载荷卸去（简称卸载），则在卸载过程中，力与变形按线性规律减少，且其间的比例关系与弹性阶段基本相同。载荷全部卸除以后，试件所产生的变形一部分消失，而另一部分则残留下来，试件不能完全恢复原状。在屈服阶段，试件已经有了明显的塑性变形。因此，过了弹性阶段以后，拉伸图曲线上任一点处对应的变形，都包含着弹性变形le及塑性变形lp两部分（见图2）。

第 Ⅳ 阶段  当拉力继续增大达某一确定数值时，可以看到，试件某处突然开始逐渐局部变细，形同细颈，称颈缩现象。颈缩出现以后，变形主要集中在细颈附近的局部区域。因此，第 Ⅳ 阶段称为局部变形阶段。局部变形阶段后期，颈缩处的横截面面积急剧减少，试件所能承受的拉力迅速降低，最后在颈缩处被拉断。若用d1及l1分别表示断裂后颈缩处的最小直径及断裂后试件工作段的长度，则d1及l1与试件初始直径d 0及工作段初始长度l0相比，均有很大差别。颈缩出现前，试件所能承受的拉力最大值，称为最大载荷，用Fb表示。

2）低碳钢拉伸时的力学性能

    低碳钢的拉伸图反映了试件的变形及破坏的情况，但还不能代表材料的力学性能。因为试件尺寸的不同，会使拉伸图在量的方面有所差异，为了定量地表示出材料的力学性能，将拉伸图纵、横坐标分别除以A0及l0，所得图形称为应力 - 应变图（- 图）， = F/A0， = l/l。图3为低碳钢的应力 – 应变图。由图可见，应力 – 应变图的曲线上有n个特殊点（如图中a、b、c、e等），当应力达到这些特殊点所对应的应力值时，图中的曲线就要从一种形态变到另一种形态。这些特殊点所对应的应力称为极限应力，材料拉伸时反映强度的一些力学性能，就是用这些极限应力来表示的。从应力 – 应变图上，还可以得出反映材料对弹性变形抵抗能力及反映材料塑性的力学性能。下面对拉伸时材料力学性能的主要指标逐一进行讨论。

    比例极限及弹性模量E  应力 – 应变曲线上o a段，按一般工程精度要求，可视为直线，在a点以下，应力与应变成正比。对应于a点的应力，称为比例极限，用E表示比例常数，则有

这就是虎克定律，其中比例常数E表示产生单位应变时所需的 应力，是反映材料对弹性变形抵抗能力的一个性能指标，称为抗拉弹性模量，简称弹性模量。不同材料，其比例极限和弹性模量E也不同。例如，低碳钢中的普通碳素钢A3，比例极限约200MPa，弹性模量约200GPa。

    弹性极限  是卸载后不产生塑性变形的最大应力，在图3中用b点所对应的应力表示。实际上低碳钢的弹性极限与比例极限十分接近，可以认为，对低碳钢来说，=。

    屈服点  等于屈服载荷Fs除以试件的初始横截面面积A0，即

    从图3可见，屈服阶段中曲线呈锯齿形，应力上下波动，锯齿形最高点所对应的应力称为上屈服点，最低点称为下屈服点。上屈服点不太稳定，常随试验状态（如加载速率）而改变。下屈服点比较稳定（如图3中的c点），通常把下屈服点所对应的应力作为材料的屈服点（参看GB228-76《金属拉力试验法》）。应力达屈服点时，材料将产生显著的塑性变形。

    强度极限或抗拉强度  图4-3中e点的应力等于试件拉断前所能承受的最大载荷Fb除以试件初始横截面面积A 0，即

当横截面上的应力达强度极限时，受拉杆件上将开始出现颈缩并随即发生断裂。

    屈服点和抗拉强度是衡量材料强度的两个重要指标。普通碳素钢A3的屈服点约为=220MPa，抗拉强度约为 =420MPa。

    伸长率  为试件拉断后，工作段的残余伸长量lR=l1l0与标距长度l0的比值，通常用百分数表示，即

伸长率 表示试件在拉断以前，所能进行的塑性变形的程度，是衡量材料塑性的指标。标距长度对伸长率有影响，因此，对用5倍试件及10倍试件测得的伸长率分别加注解标5及10字样，即分别用 5及 10表示，以示区别。普通碳素钢A3的伸长率可达 5=27%以上，在钢材中是塑性相当好的材料。工程上通常把静载常温下伸长率大于5%的材料称为塑性材料，金属材料中低碳钢是典型的塑性材料。

    截面收缩率  用试件初始横截面面积A0减去断裂后颈缩处的最小横截面面积A1，并除以A0所得商值的百分数表示，即

普通碳素钢A3的截面收缩率约为 = 55%。

3．冷作硬化现象

图4a表示低碳钢的拉伸图。设载荷从零开始逐渐增大，拉伸图曲线将沿Odef线变化直至f点发生断裂为止。前已述及，经过弹性阶段以后，若从某点（例如d点）开始卸载，则力与变形间的关系将沿与弹性阶段直线大体平行的dd 线回到d 点。若卸载后从d 点开始继续加载，曲线将首先大体沿dd线回至d点，然后仍沿未经卸载的曲线def变化，直至f点发生断裂为止。

    可见在再次加载过程中，直到d点以前，试件变形是弹性的，过d点后才开始出现塑性变形。比较图4中a、b所示的两条曲线，说明在第二次加载时，材料的比例极限得到提高，而塑性变形和伸长率有所降低。在常温下，材料经加载到产生塑性变形后卸载，由于材料经历过强化，从而使其比例极限提高、塑性性能降低的现象称为冷作硬化。

    冷作硬化可以提高构件在弹性范围内所能承受的载荷，同时也降低了材料继续进行塑性变形的能力。一些弹性元件及操纵钢索等常利用冷作硬化现象进行预加工处理，以使其能承受较大的载荷而不产生残余变形。冷压成形时，希望材料具有较大塑性变形的能力。因此，常设法防止或消除冷作硬化对材料塑性的影响，例如，在工序间进行退火等。

2.  铸铁的拉伸实验

    静载常温下伸长率小于5%的材料习惯上称为脆性材料。砖、石、玻璃、水泥、灰铸铁及某些高强度钢等都属于脆性材料。灰铸铁（简称铸铁）拉伸时，断裂后测得的伸长率尚不及1%，在金属材料中，是一种典型的脆性材料。图4-5为铸铁拉伸时的应力 – 应变图。由图可见，铸铁拉伸时，没有屈服阶段，也没有颈缩现象，反映强度的力学性能只能测得强度极限，而且拉伸时强度极限的值较低。铸铁的应力 – 应变图没有明显的直线段，通常在应力较小时，取图上的弦线近似地表示铸铁拉伸时的应力 – 应变关系，并按弦线的斜率近似地确定弹性模量E。由于铸铁的抗拉强度较差，一般不宜选做承受拉力的构件。抗拉强度差，这是脆性材料共同的特点。

3.  低碳钢和铸铁的压缩实验

    图4-6中，曲线1表示低碳钢试件压缩时的应力 –应变图，曲线2为拉伸时的应力 – 应变图。两个图形曲线在屈服阶段以前基本重合，即低碳钢压缩时，弹性模量E、屈服点均与拉伸时大致相同。过了屈服阶段，继续压缩时，试件的长度愈来愈短，而直径不断增大，由于受试验机上下压板摩擦力的影响，试件两端直径的增大受到阻碍，因而变成鼓形。压力继续增加，鼓形高度减小，直径愈益增大，最后被压成薄饼，而不发生断裂，因而低碳钢压缩时测不出强度极限。由于低碳钢压缩时的主要力学性能与拉伸时大体相同，所以一般通过拉伸试验即可得到其压缩时的主要力学性能。因此，对低碳钢来说，拉伸试验是基本的试验。

    图4-9为铸铁压缩时的应力 – 应变图。与拉伸时相比，铸铁压缩时强度极限很高，例如，HT30-54压缩时的强度极限约为拉抻时强度极限的4倍。抗压强度远大于抗拉强度，这是铸铁力学性能的重要特点。铸铁试件受压缩发生断裂时，断裂面与轴线大致成45的倾角（图4-7），这表明铸铁试件受压时断裂是因最大切应力所致。

    顺便指出，混凝土及石料等非金属脆性材料进行压缩试验时，常采用立方体形状的试件。这类材料受压破坏的形式与试件端面所受摩擦阻力有关。例如，压缩时若在端面涂以润滑剂，试件将沿纵向开裂，而不涂润滑剂时，压坏后将呈对接的截锥体形。两种情况下测得的抗压强度极限亦不相同。因此，对这类材料进行压缩实验时，除应注意采用规定的试件形状及尺寸外，还须注意端面的接触条件。

 三、  常见工程材料的应力 – 应变曲线

    各种材料均可通过拉伸试验测定其力学性能，并绘制应力 – 应变图。图4-9示意表示几种塑性材料的应力 – 应变图。由图可见，一些塑性材料的应力 – 应变图中没有明显的屈服阶段。对于没有明显屈服阶段的塑性材料，通常人为地规定，把产生0.2%残余应变时所对应的应力作为名义屈服点，并用表示（图4-10）。通常对于没有明显屈服阶段的材料，手册中列出的即是指的名义屈点。表4-1给出了几种常用金属材料拉伸时的力学性能。关于材料更详尽的资料，可查阅有关国家标准、部标准或企业标准以及有关资料手册等。

表1  几种常用材料的主要力学性能

    高分子材料是一种常用的工程材料，其种类很多，它们的力学性能有很大差异。主要分这样几类，一类为硬而脆的高分子材料，如聚苯乙烯、有机玻璃等，聚苯乙烯的应力  应变曲线示在图4-11中；第二类为具有一定强度和塑性的结晶态高分子材料，如尼龙、聚碳酸脂等，尼龙的应力  应变曲线见图4-11；第三类为高弹性材料，如橡胶等。

    需要指出，结晶态高分子材料，拉伸时颈缩现象不是发生在强化阶段之后，而是在屈服的开始。但颈缩后不立即发生断裂，仍能承受很大的应变。

    近年来，复合材料以其诸多优点广泛应用于各个工程领域。图4-12为某种碳 / 环氧（碳纤维增强环氧树脂基体）单层纤维复合材料沿纤维方向和垂直纤维方向拉伸时的应力  应变曲线，由图可见，材料的力学性能随加力方向变化，即为各向异性，其沿着纤维方向的抗拉强度和弹性模量均远大于垂直纤维方向的值。碳纤维和玻璃纤维的单向复合材料的力学性能列于表4-2中。

表2  单向复合材料的力学性能

    注：Vf 是纤维在复合材料中所占体积的百分数

§2-7强度条件·安全因数·许用应力

一、许用应力

前述试验表明，当正应力达到强度极限时，会引起断裂；当正应力达到屈服应力时，将产生屈服或出现显著塑性变形。构件工作时发生断裂显然是不容许的，构件工作时发生屈服或出现显著塑性变形一般也是不容许的。所以，从强度方面考虑，断裂是构件破坏或失效的一种形式，同样，屈服或出现显著塑性变形，也是构件失效的一种形式，一种广义的破坏。
　　根据上述情况，通常将强度极限与屈服应力统称为材料的极限应力，并用表示。对于脆性材料，强度极限为其唯一强度指标，因此以强度极限作为极限应力；对于塑性材料，由于其屈服应力小于强度极限，故通常以屈服应力作为极限应力。
　　根据分析计算所得构件之应力，称为工作应力。在理想的情况下，为了充分利用材料的强度，似可使构件的工作应力接近于材料的极限应力。但实际上不可能的，原因是：
　　1、作用在构件上的外力常常估计不准确；
　　2、构件的外形与所受外力往往比较复杂，进行分析计算常常需要采用一些简化，因此，计算所得应力（即工作应力）通常均带有一定程度的近似性；
　　3、实际材料的组成与品质等难免存在差异，不能保证构件所用材料与标准试样具有完全相同力学性能，更何况由标准试样测得的力学性能，本身也带有一定分散性，这种差别在脆性材料中尤为显著；等等。
　　所有这些不确定因素，都有可能使构件的实际工作条件比设想的要偏于不安全的一面。
　　除以上原因外，为了确保安全，构件还应具有适当的强度储备，特别是对于因破坏将带来严重后果的构件，更应给予较大的强度储备。
　　由此可见，构件工作应力的最大容许值，称为材料的许用应力，并用[ ]表示。许用应力与极限应力的关系为

式中，n为大于1的因数，称为安全因数。
　　如上所述，安全因数是由多种因素决定的。各种材料在不同工作条件下的安全因数或许用应力，可从有关规范或设计手册中查到。在一般静强度计算中，对于塑性材料，按屈服应力所规定的安全因素ns，通常取为1.5~2.2；对于脆性材料，按强度极限所规定的安全因数 ，通常取为3.0~5.0，甚至更大。
　　前已指出，构件在交变应力作用下可能发生疲劳破坏，所以疲劳破坏也是构件破坏或失效的一种形式。关于构件在交变应力作用下的疲劳强度问题，将在本书后面详细讨论。

二、 强度条件

根据以上分析，为了保证拉压杆在工作时不致因强度不够而破坏，杆内的最大工作应力不得超过材料的许用应力[]，即要求

上述判据称为拉压杆的强度条件。对于等截面拉压杆，上式则变为

利用上述条件，可以解决以下几类强度问题。
　　1、校核强度
　　当已知拉压杆的截面尺寸、许用应力和所受外力时，通过比较工作应力与许用应力的大小，以判断该杆在所受外力作用下能否安全工作。
　　2、选择截面尺寸
　　如果已知拉压杆所受外力和许用应力，根据强度条件可以确定该杆所需横截面面积。例如对于等截面拉压杆，其所需横截面面积为

3、确定承载能力
　　如果已知拉压杆的截面尺寸和许用应力，根据强度条件可以确定该杆所能承受的最大轴力，其值为

最后还应指出，如果工作应力超过了许用应力[]，但只要超过量（即 与[]之差）不大，例如不超过许用应力的5%，在工程计算中仍然是允许的。

例 已知三铰屋架如图，承受竖向均布载荷，载荷的分布集度为：q =4.2kN/m，屋架中的钢拉杆直径 d =16 mm，许用应力[s]=170M Pa。试校核刚拉杆的强度。

解：① 整体平衡求支反力 

② 局部平衡求 轴力：    

③应力： 

④强度校核与结论： 

此杆满足强度要求，是安全的。

例 如图所示空心圆截面杆，外径D=20mm，内径d=15mm，承受轴向载荷F=20kN作用，材料的屈服应力，安全因数。试校核杆的强度。

　　解：杆件横截面上的正应力为

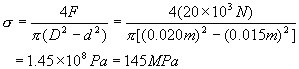
　　根据公式可知，材料的许用应力为

可见，工作应力小于许用应力，说明杆件能够安全工作。

例 杆系结构，如图所示，已知杆AB、AC材料相同，MPa，横截面积分别为mm2，mm2，试确定载荷P的最大值。

解：（1）由平衡条件计算实际轴力，设AB杆轴力为，AC杆轴力为。

对于节点A，由得

                            （1）

由得

                          （2）

由强度条件计算容许轴力

                    kN

                    kN

由于AB、AC杆不能同时达到最大容许轴力，则将，代入（2）式，解得

  kN

这个解显然是错误的。

正确的解应是将（1）、（2）式联解

（2）根据强度条件计算实际轴力达到容许轴力时各杆对应的容许载荷，即，时所对应的载荷，由

  kN

所以

  kN

则

  kN

而

  kN

所以

  kN

则

  kN

要保证AB、AC杆的强度，应取小值，即，因而得

  kN

§2-8   应力集中的概念

工程实际中，由于结构或功能上的需要，构件常制成阶梯形状（图5-9a）、带有圆孔（图5-9b）或切槽等，使构件截面尺寸或形状发生突变。较精确的理论分析和实验表明，在外力作用下，弹性体形状或截面尺寸发生突变的局部区域应力急剧增大，这种现象称为应力集中。例如，图5-9a所示的阶梯形杆件，发生突变的截面处应力非均匀分布， 、 处应力显著增大；图5-9b所示为一带有圆孔的薄板过圆孔直径的横截面上应力分布情况。由图可见，在靠近孔边的 、 处应力显著增大。

设发生应力集中的横截面上的最大应力为 ，同一横截面上的平均应力为σn，则比值

                                                                 （5-2）

称为理论应力集中系数。它反映了应力集中的程度，是一个大于1的系数。截面尺寸改变得越急剧，角越尖，孔越小，应力集中的程度就越严重。工程中，一些常见情况下的理论应力集中系数已编制成图表列于有关手册之中。

不同材料对应力集中的敏感程度是不同的。在静载荷作用下，对有着明显屈服阶段的塑性材料，当局部区域的最大应力达到屈服点时，该局部区域将产生塑性变形，随着外力的增加，该区域的应力将暂缓增加，而邻近各点的应力将继续増大，屈服区域不断扩大，直至相继达到屈服点。即随着外力增加，横截面上应力逐渐趋于均匀，而缓和了应力集中。而脆性材料，由于没有屈服点，应力集中处的应力首先达到强度极限而在该处开裂。所以，对脆性材料的构件，应考虑应力集中的影响。但像灰口铸铁一类的脆性材料，其内部组织上的缺陷所产生的应力集中是主要因素，而对因截面突变所引起的应力集中并不敏感，一般不予考虑。

受冲击载荷及随时间作周期性变化的载荷作用时，不论是用塑性材料还是用脆性材料制成的构件应力集中的影响均不可忽视，这一问题将在以后讨论。