第九章 压杆稳定

§9-1 压杆稳定性的概念

一、引言

工程中有许多细长的轴向压缩杆件，例如，气缸或油缸中的活塞杆、内燃机连件、建筑结构中的立柱、火箭的级间连接支杆等。材料力学中统称为压杆或柱。前面研究直杆轴向压缩时，认为杆是在直线形态下维持平衡，杆的失效是由于强度不足而引起的。事实上，这样考虑，只对短粗的压杆才有意义，而对细长的压杆，当它们所受到的轴向外力远未达到其发生强度失效时的数值，可能会突然变弯而丧失了原有直线形态下的平衡而引起失效。它是不同于强度失效的又一种失效形式。

受压变弯的原因：（1）压秆在制造时其轴线存在初曲率。（2）合外力作用线与杆轴线没有重合。（3）材料的不均匀性。

二、“中心受压理想直杆”力学模型及稳定的概念

力学模型：材料绝对理想；轴线绝对直；压力绝对沿轴线作用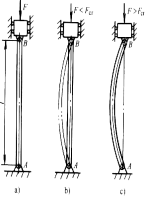　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
试验：取如图所示两端铰支均质等直细长杆，加轴向压力F，压杆呈直线形态平衡。现在，若此压杆受到一很小的横向干扰力。(例如，轻轻地推一下)，则压杆弯曲，如图 a中虚线所示。当横向干扰力解除后，会出现下述两种情况：

    1) 当轴向压力F小于某一数值时，压杆又恢复到原来的直线平衡形态，如图 b所示。（稳定平衡）

    2) 当轴向压力F增加到这一数值时，虽然干扰力已解除，但压杆不再恢复到原来的直线平衡形态，而在微弯曲的形态下平衡，如图 c所示。（不稳定平衡）

可见，压杆的原来直线形态平衡是否稳定，与所受轴向压力F的大小有关；当轴向压力F由小逐渐增加到某一个数值时，压杆的直线形态平衡由稳定过渡到不稳定。压杆的直线形态平衡由稳定过渡到不稳定所受的轴向压力的界限值，称为压杆的临界力，用Fcr表示。当压杆所受的轴向压力F达到临界力Fcr时，其直线形态的平衡开始丧失，我们称压杆丧失了稳定性，简称失稳。研究压杆稳定性的关键是寻求其临界力的值。

§9-2细长中心受压直杆临界力的欧拉公式

假设两端球形铰支的等直细长压杆所受的轴向压力刚好等于其临界力 ，并且已经失稳而在微弯曲状态下保持平衡，如图所示。假想沿任意x截面将已挠曲的压杆截开，保留部分如图所示。由保留部分的平衡得
　　　　　         （a）     
式（a）中，轴向压力Fcr取绝对值，这样在图示坐标系中弯矩M与挠度 的符号总相反，故式中加了一个负号。当杆内应力不超过材料的比例极限时，根据挠曲线的近似微分方程得
　　　　　 （b）                              　　　　　
令
　　　　　                            （c）
则式（b）改写为
　　　　　            　　　 （d）
此微分方程的通解为
　　　　　                （e）  
式中C1、C2为积分常数，由压杆的边界条件确定。
此压杆两端铰支，边界条件为
　　　　　 x=0时， =0                       （f）
　　　　　 x=l 时， =0                       (g)
由（f）、(g)得
　　　　　 C2=0，C1SinKl=0                             
积分常数C1不能等于零，否则挠曲线方程 ≡0，这意味着压杆可稳定地保持着直线平衡形态，与假定压杆已失稳相矛盾。因此只有
　　　　　 SinKl=0                        　　（h）
式（h）的解为
　　　　　 Kl=nπ        （n =0，1，2，3…）
　　　　　
由式(c)
　　　　　
得           （n =0，1，2，3…）    （i）             
因为n可取0，1，2，3…中的任一整数，所以式(i)表明,使压杆保持曲线形态平衡的压力,在理论上是多值的。而在这些压力中，使压杆保持微弯曲的最小轴向压力，才是其临界力。取n =1，得两端铰支细长压杆的临界力公式
　　　　　                         （9-1）
式（9-1）又称为欧拉公式。
在此临界力作用下，K= ，则式（e）可写成
　　　　　                          （j）
可见，两端铰支细长压杆失稳后，挠曲线是条半波正弦曲线。

§9-3 不同杆端约束下细长压杆的临界力

工程中的压杆，两端会有各种不同的约束。从上述推导临界力的过程可看出，约束条件不同，压杆的临界力也不同，即杆端约束对临界力有影响。
    在其它约束情况下，可用上述静力法求临界力，也可用如下简捷的方法求临界力。如图是一端固定、一端自由长为l 的压杆。根据约束，失稳后挠曲线形状如图 b中曲线AB。将失稳后的挠曲线AB以固定端B为对称点向下延长至A/。延长后的挠曲线AA/是一条半波正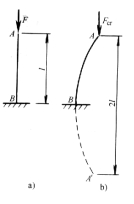弦曲线，与两端铰支压杆失稳后的挠曲线形状一样。这样就比拟得到，一端固定、一端自由长为l 的压杆的临界力与两端铰支长为2 l压杆的临界力相同。即
　　
用这种比较失稳后挠曲线形状的方法，同样会得到其它约束情况下压杆的临界力公式，这些公式可统一写成
　　　                           （  9-2  ）    

上式称为欧拉公式的一般形式。由式（9-2）可见，杆端约束对临界力的影响表现在系数μ上。称μ为长度因数；μl为压杆的相当长度，表示长为l 的压杆折算成两端铰支杆后的长度。几种常见约束情况下的长度系数μ列于表9-1中。

表9-1   压杆的长度因数

§9-4 欧拉公式的应用范围   临界应力总图 

一、欧拉公式的应用范围

将式(9-2)的两端同时除以压杆的横截面面积A，得到压杆的临界应力
　　　　　　                                
引入截面的惯性半径
　    　                                    　  　　　(9-3)
这样式(a)可改写为
　　 　                            　　　　　　 (9-4)
式 (9-4)是用应力形式表示的欧拉公式。式中
　　　　　                           　　　　　　　　　(9-5)
λ称为压杆的柔度，是一个无量纲的量。
    由式 (9-4)可知，相同材料压杆的临界应力取决于压杆的柔度 。而压杆的柔度与压杆的长度、约束条件以及截面的形状、尺寸有关。
    在推导欧拉公式时，曾使用了挠曲线的近似微分方程式。而这个方程式是建立在材料服从虎克定律基础上的。试验已证实，当临界应力不超过材料的比例极限 时，欧拉公式

才适用，即
　　　　　 ≤
或　　　　 ≥
欧拉公式成立时，压杆柔度 的最小值用 表示，即
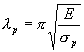　　　　　                        　　　　　　　 　(9-6)
式(9-6)说明，极限值 只与压杆的材料有关。只有 ≥ 时，才能用欧拉公式计算压杆的临界力或临界应力。

(1)细长杆或大柔度压杆：　 ≥ ,是在材料比例极限内的稳定性问题，临界应力用欧拉公式计算；

(2)中柔度压杆：λ≤<

    对于由合金钢、铝合金、铸铁与松木等材料制作的中柔度压杆 ，可采用直线型经验公式计算临界应力，该公式的一般表达式为
　 　　　　　                          　（9-7）
式中 、 为与材料性质有关的常数。在使用上述直线公式时，柔度 存在一最低界限值 ，其值与材料的压缩极限应力 有关。因为对于很小柔度的短压杆，当它所受到的压应力达到压缩极限应力 时，压杆已因强度不足而失效。例如，塑性材料的压缩极限应力为屈服点 ，于是，在式（9-7）中，令 得

                          （9-8）
　与 一样也是只与材料性质有关的常数。几种常用材料的 、 和 、 值如表9-2所示。

压杆的临界应力随着压杆的柔度变化情况可用如图 的曲线表示，此曲线称为临界应力总图。

 (3)小柔度压杆： <λ　是短粗杆，将发生强度失效，而不发生失稳破坏。 临界应力就是屈服点 或强度极限

表9-2    几种常用材料的 、 、 、

例 如图为一用№20a工字钢制成的压杆，材料为Q235钢，E=200GPa，σp=200MPa，压杆的长度l=5m。求此压杆的临界力。
解：求压杆的柔度
由附录 中的型钢表查得     =8.51cm， =2.12cm， =35.5cm2
压杆在 最小的纵向平面内柔度最大，临界力最小。因而，压杆若失稳一定发生在压杆柔度最大的纵向平面内。最大的柔度
　　　　　　　
计算
　　　　　　
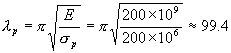
求临界力
因为 > ，此压杆是细长杆，用欧拉公式计算临界应力
　　　　　　  
临界力    

§9-5   压杆的稳定性计算 压秆的合理截面

一、 稳定性条件

压杆的临界力Fcr与压杆实际承受压力F的比值，称为压杆的工作安全系数，用nst表示。压杆在工作压力F作用下不失稳的条件是：压杆的工作安全系数nst应不小于规定的许用稳定安全系数[nst]，即
  　　　　　 ≥                                 　 （9-9）
式（16-14）称为压杆的稳定性条件。由式（9-9）便可对压杆进行稳定性设计，在工程中主要是稳定性校核。通常对许用稳定安全系数[nst]规定得比强度安全系数要高，其原因是，对于受压杆件存在着一些难以避免的因素（例如，压杆的初弯曲、压杆的偏心、不完善的端部条件以及材料不均匀等），这些因素对压杆稳定性的影响远远超过对强度的影响。式（9-9）是用安全系数形式表示的稳定性条件。工程中还常用应力形式来表示稳定性条件，即
　　　　　 ≤                               　　 　(9-10)
式中 ，称为稳定许用应力。因为临界应力 随柔度 而变化，另外，对不同柔度的压杆又规定了不同的安全系数[nst]，因而，稳定许用应力[σ]st与强度许用应力[σ]不同。

工程实际中，压杆设计常用的方法是，将压杆的稳定许用应力[σ]st，用材料的许用压应力[σ]乘以一个随压杆柔度 变化的系数 来表示，即
　　　　　                                　(9-11)
这样，就可以将压杆柔度 对σcr和nst的影响用一个系数 = 来表示。λ越大 越小，且对于稳定性问题， 总是小于1（而强度问题 =1）。所以 称为压杆的稳定因数。书中给出了Q235钢稳定因数的值。
用稳定因数表示的稳定性条件为
              　　≤                       　　　（9-12）

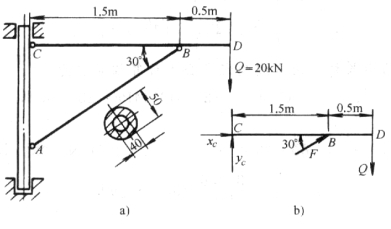例  简易吊车摇臂如图 所示。两端铰支的AB杆由钢管制成，材料为Q235钢，其强度许用应力[σ]=140MPa，试校核AB杆的稳定性。

解：求AB杆所受的轴向压力，为此取CD杆为研究对象，如图 所示。
由                  　  ，
　　　　
得  

AB杆横截面的惯性半径
　　　　　　
AB杆的柔度
　　　　　　
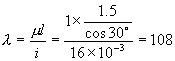
查表得稳定因数                           
　　　　　     　　　
稳定许用应力
　　　　　　
AB杆的工作应力
　　　　　　　
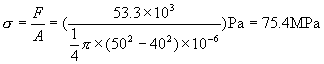
　　　　　        　　　 σ<[σ]st
AB杆稳定。

二、提高压杆承载能力的措施

压杆的稳定性取决于临界载荷的大小。由临界应力图可知，当柔度减小时，则临界应力提高，而，所以提高压杆承载能力的措施主要是尽量减小压杆的长度，选用合理的截面形状，增加支承的刚性以及合理选用材料。现分述如下：

1．减小压杆的长度

减小压杆的长度，可使降低，从而提高了压杆的临界载荷。工程中，为了减小柱子的长度，通常在柱子的中间设置一定形式的撑杆，它们与其他构件连接在一起后，对柱子形成支点，限制了柱子的弯曲变形，起到减小柱长的作用。对于细长杆，若在柱子中设置一个支点，则长度减小一半，而承载能力可增加到原来的4倍。

2．选择合理的截面形状

压杆的承载能力取决于最小的惯性矩I，当压杆各个方向的约束条件相同时，使截面对两个形心主轴的惯性矩尽可能大，而且相等，是压杆合理截面的基本原则。因此，薄壁圆管 正方形薄壁箱形截面是理想截面，它们各个方向的惯性矩相同，且惯性矩比同等面积的实心杆大得多。但这种薄壁杆的壁厚不能过薄，否则会出现局部失稳现象。对于型钢截面（工字钢、槽钢、角钢等），由于它们的两个形心主轴惯性矩相差较大，为了提高这类型钢截面压杆的承载能力，工程实际中常用几个型钢，通过缀板组成一个组合截面，如图 所示。并选用合适的距离a，使，这样可大大的提高压杆的承载能力。但设计这种组合截面杆时，应注意控制两缀板之间的长度，以保证单个型钢的局部稳定性。

3．增加支承的刚性

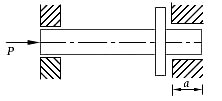对于大柔度的细长杆，一端铰支另一端固定压杆的临界载荷比两端铰支的大一倍。因

此，杆端越不易转动，杆端的刚性越大，长度系数就越小，图15-9所示压杆，若增大杆右端止推轴承的长度a，就加强了约束的刚性。

 4．合理选用材料

对于大柔度杆，临界应力与材料的弹性模量E成正比。因此钢压杆比铜、铸铁或铝制压杆的临界载荷高。但各种钢材的E基本相同，所以对大柔度杆选用优质钢材比低碳钢并无多大差别。对中柔度杆，由临界应力图可以看到，材料的屈服极限和比例极限越高，则临界应力就越大。这时选用优质钢材会提高压杆的承载能力。至于小柔度杆，本来就是强度问题，优质钢材的强度高，其承载能力的提高是显然的。