直流数字电压的不确定度计算
浅谈EXCEL在检定工作中应用之三
直流数字电压的不确定度计算分析的数学模型已经确定,只需用EXECL按步骤编程。操作如下: (图1)
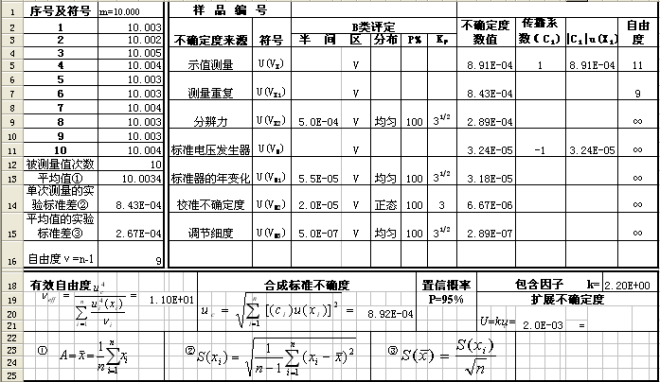
1.图1为四位半数字万用表,在10V处校准点不确定度的计算表格。设置在EXCEL工作表(表1)中,把数据处理设在工作(表2)中。
2.测量重复由单次测量的实验标准差公式获得(在浅谈EXCEL之一叙述过),并索引到工作表(表2)中:H5=Sheet1!F14=8.43E-04,自由度为9。
3. 引用不确定度计算分析列表如下:
不确定度 来源 | 计算公式 | EXCEL编程 |
分辨力 | u(VN3)=0.5/ | H7=G7/1.732=2.89E-04,G7=0.5 |
示值测量 | 自由度为:υ(Vx2)=∞ 以上两项各不相关,合成得: u2(Vx)= (u2(Vx1)+ u2(Vx2))1/2=0.891(mV) 自由度为:υ(Vx)= u4(Vx1)/{ u4(Vx1)/ υ(Vx1)+ u4(Vx2)/ υ(Vx2)}=11 | 两项各不相关合成 H3=SQRT(H7^2+H5^2)=8.91E-04 自由度为 H2=INT((H3^4/H5^4)*9+0.5)=11
|
标准器的 年变化 | u(VN1)=55/ | H11=G11/1.732=3.18E-05 G11=5.5E-05 |
校准 不确定度 | u(VN2)=20/3=6.67(μV) | H13=G13/3=6.67E-06 G13=2.0E-05 |
调节细度 | u(VN3)=0.5/ | H14=G14/1.732=22.89E-07 G14=5.0E-07 |
标准电压 发生器 | u(VN)=(u2(VN1)+ u2(VN2)+ u2(VN3))1/2 =32.5(μV) | H9=SQRT(H11^2+H13^2+H14^2) =3.24E-05 |
有效度 自由度 | υeff=1.10E+01 注1 | H15=(H16^4/H3^4)*H2=1.10E+01 H15中数据输入查表《t分布在不同置信概率p与自由度ν的tp(ν)值(t值)》单元。注2 |
合成标准 不确定度 | uC(y)=( | H16=SQRT(H3^2+H9^2) = 8.92E-04 |
扩展 不确定度 | U0.95=2.20×8.92E-04=2(mV) | H18=H17*H16=2.0E-04 H17是《t分布在不同置信概率p与自由度ν的tp(ν)值(t值)》查表得到扩展因子。 |
由EXCEL计算出的各项数据结果,再影像到不确定度的计算表各个相应项目中。
整个过程只需要输入10个数据,大大的缩短了计算时间,提高计算的可靠性和工作效率。可是在实际工作中,数字万用表种类较多,位数和分辨力各不相同。该计算过程只能反映初步编程框架 ,A类不确定度计算还需要进一步优化,具有判断不同位数和分辨力的功能,才能完善A类的计算,这些将在下文叙述。
注1:υeff=u4(y)/ 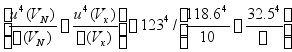
注2:查表《t分布在不同置信概率p与自由度ν的tp(ν)值(t值)》在浅谈EXCEL之二叙述过。