第九章 稳恒电流的磁场
第九章 稳恒电流的磁场
稳恒电流:导体中电流不随时间变化(也叫直流电)。
§9-1基本磁现象 安培假说
人们对磁现象的研究是很早的,而且开始时是与电现象分开研究的。发现电、磁现象之间存在着相互联系的事实,首先应归功于丹麦物理学家奥斯特。他在实验中发现,通有电流的导线(也叫载流导线)附近的磁针,会受力而偏转。1820年7月21日,他在题为《电流对磁针作用的实验》小册子里,宣布了这个发现。这个事实表明电流对磁铁有作用力,电流和磁铁一样,也产生磁现象。
1820年8月,奥斯特又发表了第二篇论文,他指出:放在马蹄形磁铁两极间的载流导线也会受力而运动。这个实验说明了磁铁对运动的电荷有作用力。
1820年9月,法国人安培报告了通有电流的直导线间有相互作用的发现,并在1820年底从数字上给出了两平行导线相互作用力公式。这说明了二者的作用是通过它们产生的磁现象进行的。
综上可知,电流是一切磁现象的根源。
为了说明物质的磁性,1822年安培提出了有关物质磁性的本性的假说,他认为一切磁现象的根源是电流,即电荷的运动,任何物体的分子中都存在着回路电流,成为分子电流。分子电流相当于基元磁铁,由此产生磁效应。安培假说与现代物质的电结构理论是符合的,分子中的电子除绕原子核运动外,电子本身还有自旋运动,分子中电子的这些运动相当于回路电流,即分子电流。
磁场的应用十分广泛。如:电子射线 、回旋加速器、质谱仪、真空开关等都利用了磁场。
§9-2 磁场 磁感应强度 磁力线 磁通量
一、磁场
1、磁场:运动电荷或电流周围也有一种场,称为磁场。
2、磁场的主要表现
(1)力的表现:磁场对运动电荷或载流导体有作用力。
(2)功的表现:磁场对载流导体能做功。
3、实验表明:磁场与电场一样,既有强弱,又有方向。
 二、磁感应强度
二、磁感应强度
为了描述磁场的性质,如同在描述电场性质时引进电场
强度时一样,也引进一个描述磁场性质的物理量。
下面从磁场对运动电荷的作用力角度来定义磁感应强度。
设E、![]() 、
、![]() 为电荷电量、速度、受磁场力。实验结果为:
为电荷电量、速度、受磁场力。实验结果为:
1、![]() ,
,![]() ;
;
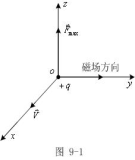
2、![]() 与
与![]() 同磁场方向夹角有关,当
同磁场方向夹角有关,当![]() 与磁场平行时,
与磁场平行时,![]() =0;当
=0;当![]() 与磁场垂直时,
与磁场垂直时,![]() 。如
。如![]() 、磁场方向在x、y轴上,则
、磁场方向在x、y轴上,则![]() 在z轴上。
在z轴上。
可知,![]() ,可写成:
,可写成:![]() 。
。
可知:![]() 是与电荷无关而仅与O点有关即磁场性质有关的量。
是与电荷无关而仅与O点有关即磁场性质有关的量。
定义:![]() 为磁感应强度,
为磁感应强度,
大小:![]() ,
,
方向:沿![]() 方向(规定为沿磁场方向)。
方向(规定为沿磁场方向)。
说明:(1)![]() 是描绘磁场性质的物理量,它与电场中的
是描绘磁场性质的物理量,它与电场中的![]() 地位相当。
地位相当。
(2)![]() 的定义方法较多,如:也可以从线圈磁力矩角度定义等。
的定义方法较多,如:也可以从线圈磁力矩角度定义等。
(3)SI制中,![]() 单位为T(特斯拉)。
单位为T(特斯拉)。
三、磁力线
在描述电场时,引进了电力线这一辅助概念,在描述磁场中,我们也可以引进磁力线这一辅助概念。
1、![]() :方向,某点磁力线切向方向为
:方向,某点磁力线切向方向为![]() 的方向。
的方向。
大小,规定某处磁力线密度=![]() 。
。
设P点面元![]() 与
与![]() 垂直,
垂直,![]() 为
为![]() 上通过的磁力线数,则磁力线密度
上通过的磁力线数,则磁力线密度![]() ,即有:
,即有:
![]() ,
,
可知:B大处磁力线密;B小处磁力线疏。
2、磁力线性质
(1)磁力线是闭合的。这与静电场情况是截然不同的。磁场为涡旋场。
(2)磁力线不能相交,因为各个场点![]() 的方向唯一。
的方向唯一。
 四、磁通量
四、磁通量
定义:通过某一面的电力线数称为通过该面
的磁通量,用![]() 表示。
表示。
1、![]() 均匀情况
均匀情况
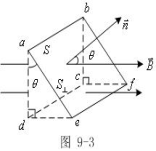 (1)平面S与
(1)平面S与![]() 垂直,如图所示,可知
垂直,如图所示,可知
(根据磁力线密度定义)
![]() (9-1)
(9-1)
(2)平面![]() 与
与![]() 夹角
夹角![]() ,如图所示,可知:
,如图所示,可知:
![]()
2、![]() 任意情况
任意情况
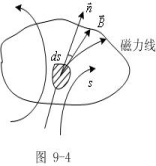 如图所示,在
如图所示,在![]() 上取面元
上取面元![]() ,
,![]() 可看成平面,
可看成平面,
![]() 上
上![]() 可视为均匀,
可视为均匀,![]() 为
为![]() 法向向量,通过
法向向量,通过![]() 的
的
磁通量为![]() ,通过S上磁通量为
,通过S上磁通量为
![]() (9-2)
(9-2)
对于闭合曲面,因为磁力线是闭合的,所以穿入闭
合面和穿出闭合面的磁力线条数相等,故![]() ,即
,即
![]() (9-3)
(9-3)
此式是表示磁场重要特性的公式,称为磁场中高斯定理。在这里,此定理只当做实验结果来接受,但是可以从磁场的基本定律和场的迭加原理严格证明。
磁通量单位:SI制中为Wb(韦伯)。
§9-3 毕奥——沙伐尔定律
我们曾经讲过,求带电体场强时,把带电体看成是由许多电荷元组成,写出电荷元的场强表达式之后,然后用迭加法求整个带电体的场强。求载流导线的磁感应强度的方法与此类似,把载流导线看作是由许多电流元组成的,如果已知电流元产生的磁感应强度,用迭加法(实验表明迭加法成立),便可求出整个线电流的磁感应强度。电流元的磁感应强度由毕奥——沙伐尔定律给出,这条定律是拉普拉斯把毕奥、沙伐尔等人的实验资料加以分析和总结得出的,故亦称毕奥——沙伐尔——拉普拉斯定律。其内容如下:
一、电流元 电流元的磁场
假设在导线上沿电流方向取![]() ,这个线元很短,可看作直线,又设导线中电流为
,这个线元很短,可看作直线,又设导线中电流为![]() ,则
,则![]() 称为电流元,如下图所示,
称为电流元,如下图所示,
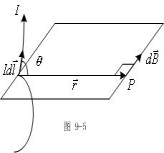
![]() 在P点产生的磁感应强度为
在P点产生的磁感应强度为![]() :
:
![]() 大小:与
大小:与![]() 成正比,与
成正比,与![]() 与
与![]() (从电
(从电
![]() 流元到P点的矢量)的夹角正弦成正比,
流元到P点的矢量)的夹角正弦成正比,
![]() 与
与![]() 大小的平方成反比,即
大小的平方成反比,即
![]() ,
,
可写成
![]() 。
。
K与磁介质和单位制选取有关。对于真空和国际单位制,![]() ,其中
,其中![]() (称为真空磁导率),
(称为真空磁导率),
![]() ,
,
![]() 方向:沿
方向:沿![]() 方向。
方向。
![]() (矢量式) (9-4)
(矢量式) (9-4)
此式是毕奥——沙伐尔定律的数学表达式。
说明: (1)毕奥——沙伐尔定律是一条实验定律。
(2)![]() 是矢量,方向沿电流流向。
是矢量,方向沿电流流向。
(3)在电流元延长线上![]() 。
。
(4)实验表明:迭加原理对磁感应强度也适用。整个导线在P点产生的![]() 为
为
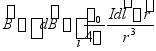 (9-5)
(9-5)
二、磁场计算
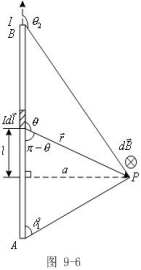
例9-1:设有一段直载流导线,电流强度为I,P点距导线为a,求P点![]() =?
=?
解:如图所示,在AB上距O点为![]() 处取电流元
处取电流元![]() ,
,![]() 在P点产生的
在P点产生的![]() 的大小为
的大小为
![]() ,
,
![]() 方向垂直指向纸面(
方向垂直指向纸面(![]() 方向)。同样可知,AB上
方向)。同样可知,AB上
所有电流元在P点产生的![]() 方向均相同,所以P点
方向均相同,所以P点
![]() 的大小即等于下面的代数积分
的大小即等于下面的代数积分
![]() ,
,
统一变量,由图知
![]()
![]() ,
,![]()
![]()
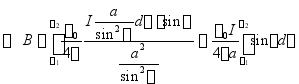
![]() ,
,![]() 垂直指向纸面。
垂直指向纸面。
讨论:(1)![]() 时,
时,![]() ,
,![]() ,
,![]() 。
。
(2)对无限长(A在O处),![]() ,
,![]() ,
,![]() 。
。
强调:(1)![]() 要记住,做题时关键找出
要记住,做题时关键找出![]() 、
、![]() 、
、![]() 。
。
(2)![]() 、
、![]() 是电流方向与P点用A、B连线间夹角。
是电流方向与P点用A、B连线间夹角。
例9-2:如图所示,长直导线折成![]() 角,电流强度为I,A在一段直导线的延长线上,C为
角,电流强度为I,A在一段直导线的延长线上,C为![]() 角的平分线上一点,AO=CO=r,求A、C处
角的平分线上一点,AO=CO=r,求A、C处![]() 。
。
解:任一点![]() 是由PO段和OQ段产生的磁感应强度
是由PO段和OQ段产生的磁感应强度![]() 、
、![]() 的迭加,即
的迭加,即![]() ,
,
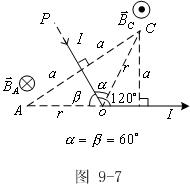 A处
A处![]() ?
?
![]() A在OQ延长线上,
A在OQ延长线上,![]()
![]() 。
。
即 ![]()
![]() :垂直指向纸面
:垂直指向纸面
![]() 大小:
大小:![]() ,
,
在此  ,
,
![]() 。
。
(2)C点的![]() =?
=?
![]()
由题知,![]() (大小和方向均相同)
(大小和方向均相同)![]()
有 ![]()
![]() 方向垂直纸面向外,
方向垂直纸面向外,
![]() 大小为:
大小为:![]()
在此 
![]() 。
。
例9-3:如图所示,一宽为a的薄金属板,其电流强度为I并均匀分布。试求在板平面内距板一边为b的P点的![]() 。
。
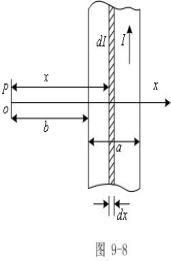 解:取P为原点,x轴过平板所在平面且与板边垂直,
解:取P为原点,x轴过平板所在平面且与板边垂直,
在x处取窄条,视为无限长载流导线,它在点产生
![]() 的方向为:垂直纸面向外,大小为
的方向为:垂直纸面向外,大小为
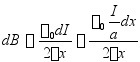 (均匀分布)
(均匀分布)
所有这样窄条在P点的![]() 方向均相同,所以求
方向均相同,所以求![]() 的大小可用下面代数积分进行:
的大小可用下面代数积分进行:
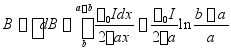 。
。
强调:(1)无限长载流导线产生磁场![]() 。
。
 (2)迭加方法要明确。
(2)迭加方法要明确。
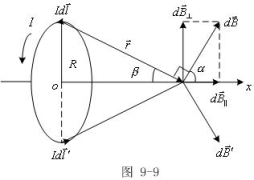
例9-4:如图所示,半径为R的载流圆线圈,
电流为I,求轴线上任一点P的磁感
应强度![]() 。
。
解:取x轴为线圈轴线,O在线圈中心,电流元
![]() 在P点产生的
在P点产生的![]() 大小为
大小为
![]()
设![]() 纸面,则
纸面,则![]() 在纸面内。
在纸面内。![]() 分成平行x轴分量
分成平行x轴分量![]() 与垂直x轴分量
与垂直x轴分量![]() 。在与
。在与![]() 在同一直径上的电流元
在同一直径上的电流元![]() 在P点产生的
在P点产生的![]() 、
、![]() ,由对称性可知,
,由对称性可知,![]() 与
与![]() 相抵消,可见,线圈在P点产生垂直x轴的分量由于两两抵消而为零,故只有平行x轴分量。
相抵消,可见,线圈在P点产生垂直x轴的分量由于两两抵消而为零,故只有平行x轴分量。
![]() ,
,
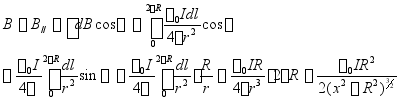
![]() 的方向沿x轴正向。
的方向沿x轴正向。
讨论:(1)x=0处, ![]() 。
。
(2)x>>R, ![]() 。
。
(3)线圈左侧轴线上任一点![]() 方向仍向右。
方向仍向右。
强调:N匝线圈: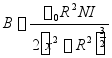 。
。
例9-5:载流螺线管的磁场。已知导线中电流为I,螺线管单位长度上有n匝线圈,并且线圈密绕,求螺线管轴线上任一点的![]() 。
。
解:如图所示,螺线管的纵剖图。此剖面图
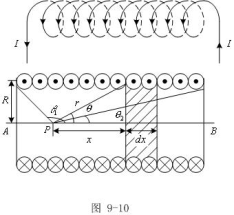 设在纸面内。在距P点为x处取长为
设在纸面内。在距P点为x处取长为![]() ,
,![]()
上含线圈为![]() 。因为螺线管上线圈饶得很密,
。因为螺线管上线圈饶得很密,
所以,![]() 段相当于一个圆电流,电流强度为
段相当于一个圆电流,电流强度为
![]() 。因此宽为
。因此宽为![]() 的圆线圈产生的
的圆线圈产生的![]() 大小为:
大小为:
![]() 。
。
所有线圈在P点产生的![]() 均向右,所以P点
均向右,所以P点![]() 为
为
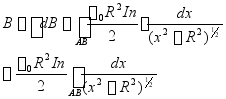 ,
,
![]() ,
,
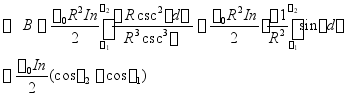 。
。
讨论:螺线管无限长时,![]() ,
,![]() ,
,![]() 。半无限长:如B在无穷远处,A轴线上的一点有
。半无限长:如B在无穷远处,A轴线上的一点有![]() ,
,![]() ,
,![]() 。
。
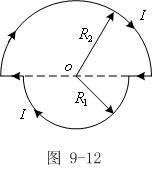
例9-6:如图所示,在纸面上有一闭合回路,它由半径为![]() 、
、![]() 的半圆及在直径上的二直线段组成,电流为I。求c圆心O处
的半圆及在直径上的二直线段组成,电流为I。求c圆心O处![]() =?(2)若小半圆绕AB转
=?(2)若小半圆绕AB转![]() ,此时O处
,此时O处![]() =?
=?
解:由磁场的迭加性知,任一点![]() 是由二半圆及直线段部分在该点产生的磁感应强度
是由二半圆及直线段部分在该点产生的磁感应强度
矢量和。此题中,因为O在直线段沿长线上,故直线段在O处不产生磁场。
(1)![]() =?
=?
小线圈在O处产生的磁场大小为:![]() (每长度相等的圆弧在O处产生的磁场大小相同);
(每长度相等的圆弧在O处产生的磁场大小相同);
方向:垂直纸面向外。
大线圈在O处产生的磁场大小为:![]() ;
;
方向:垂直纸面向里。

![]()
方向:垂直纸面向外。
(2)![]() ,可知
,可知
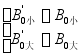 ,
,
![]() 、
、![]() 均垂直纸面向里。
均垂直纸面向里。
![]()
方向:垂直纸面向里。
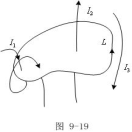
§9-4 运动电荷的磁场
我们知道,电流是一切磁现象的根源,而电流是由于电
荷定向运动形成的。可见,电流的磁场本质上是运动电荷产
生的。因此,我们可以从电流元所产生的磁场公式推导出运动电荷所产生的磁场公式。
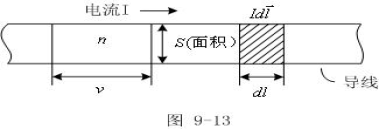
如图所示,有一段粗细均匀的直导线,电流强度为I,横截面面积为s,在其上取一电流元![]() ,它在空间某一点产生的磁感应强度为
,它在空间某一点产生的磁感应强度为 ![]()
![]() ,
,
![]() 为电流元到P点的矢径。
为电流元到P点的矢径。
按经典电子理论,金属导体中的电流是大量自由电子的定向运动形成的,为研究方便,我们可等效地认为该电流是正电荷产生的,正电荷的运动方向就是电流方向。设电荷(正电荷,下同)的电量为q,单位体积内有n个做定向运动的电荷,它们的运动速度均为恒矢![]() 。
。
下面求I=?
在导线上取长为V的一柱体,那么,在单位时间内通过此柱体右端面S的电荷数为:n(VS);
单位时间内通过此面的电量为: q(nVS)。
由电流强度定义有: I=qnVS,
故 ![]() 。
。
![]()
![]() 与
与![]() 同向,
同向, ![]()
![]()
![]()
![]() 该电流元内有定向运动的电荷数目为
该电流元内有定向运动的电荷数目为![]() 。
。
![]() 电流元内一个运动电荷产生的磁感应强度为
电流元内一个运动电荷产生的磁感应强度为
![]() ,
,
![]() (9-6)
(9-6)
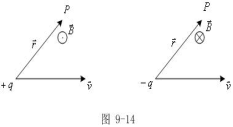 说明:(1)式中
说明:(1)式中![]() 是由运动电荷到考察点的矢量;
是由运动电荷到考察点的矢量;
(2)此式对正、负电荷均成立。
![]()
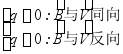 。
。
(3)研究运动电荷的磁场,在理论
上就是研究毕奥——沙伐尔定律的
微观意义。
例9-7:设电量为+q的粒子,以角速度![]() 做半径为R的匀速圆周运动,求在圆心处产生的
做半径为R的匀速圆周运动,求在圆心处产生的![]() 。
。
解:<方法一>
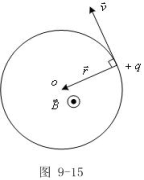 按
按![]() ,运动电荷产生的
,运动电荷产生的![]() 为
为
![]() ,
,
![]() 大小为:
大小为: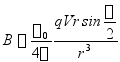 。
。
![]() r=R,
r=R,![]() ,
, ![]()
![]() 。
。
方向:垂直纸面向外。
<方法二>
用圆电流产生![]() 的公式,由电荷运动,则形成电流。在此,+q形成的电流流线与+q运动的轨迹(圆周)重合,且电流为逆时针方向,相当于一个平面圆形载流线圈。可知,
的公式,由电荷运动,则形成电流。在此,+q形成的电流流线与+q运动的轨迹(圆周)重合,且电流为逆时针方向,相当于一个平面圆形载流线圈。可知,![]() 的方向垂直纸面向外。根据平面圆形载流线圈在其中心产生
的方向垂直纸面向外。根据平面圆形载流线圈在其中心产生![]() 的大小公式,可求出
的大小公式,可求出![]() 的大小。
的大小。
设运动频率为f,可有
![]()
![]() 。
。
§9-5 安培环路定律
在电场中,我们介绍了高斯定理,由它可求出满足一定对称条件的场强,简化计算。那么,在磁场中是否也有与电场中高斯定理地位相当的规律呢?回答是肯定的,这就是安培环路定律,其内容是![]() 下面分几种情况来阐述。
下面分几种情况来阐述。
1、闭合电线L内有电流情况
设L为平面闭合曲线,所在平面与纸面垂直,直导线在纸面内并垂直L所在平面,如图(a)所示,(b)为俯视图。在L上取一线元![]() ,a、b为始、终点,
,a、b为始、终点,![]() 和
和![]() 的夹角为
的夹角为![]() ,oa=r,在a处
,oa=r,在a处![]() 的大小为
的大小为![]() ,
,![]() 的方向如图所示(
的方向如图所示(![]() 在纸面内)
在纸面内)
![]()
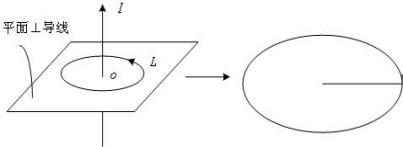
(a) (b)
图9-16
设c是![]() 与ab交点,所以
与ab交点,所以![]() 很小,
很小,![]() ,
,
![]() ,
,
当积分方向反向时,![]() ,
,
即 ![]() 。
。
当积分绕向与I的流向遵守右手螺旋定则时,上式取“+”,此时,可认为电流为正;当积分绕向与I的流向遵守左手螺旋定则时,上式取负号,此时可认为电流为负。
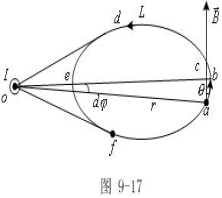 2、闭合曲线L不包含电流情况
2、闭合曲线L不包含电流情况
把上面长直导线平移到L外,则(b)图可
表示如下:
仍有
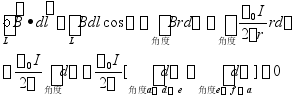 。
。
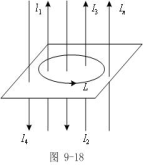 结论:L不包围电流时
结论:L不包围电流时![]() 。
。
3、在![]() 中有n条平行导线情况
中有n条平行导线情况
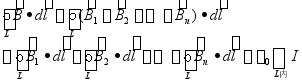 ,
,
即 ![]() (9-7)
(9-7)
此式即为安培环路定律的表达式。它表明:![]() 沿一个回路积分等于此回路内包围电流的代数和的
沿一个回路积分等于此回路内包围电流的代数和的![]() 倍。
倍。
说明:(1)如果![]() 不是平面曲线,载流导线不是直线,上式也成立。
不是平面曲线,载流导线不是直线,上式也成立。
(2)![]() ,说明了磁场为非保守场(涡旋场)。
,说明了磁场为非保守场(涡旋场)。
 (3)安培环路定律只说明
(3)安培环路定律只说明![]() 仅与L内电流有关,而与L外电流无关。对于
仅与L内电流有关,而与L外电流无关。对于![]() 是
是![]() 内外所有电流产生的共同结果。
内外所有电流产生的共同结果。
例9-8:求下列情况![]() =?
=?
解:由安培环路定律有:
![]()
![]() 。
。
例9-9:有一无限长均匀载流直导体,半径为R,电流为I均匀分布,求![]() 分布。
分布。
解:由题意知,磁场是关于导体轴线对称的。磁力线是在垂直于该轴平面上以此轴上点为圆心的一系列同心圆周,在每一个圆周上![]() 的大小是相同的。
的大小是相同的。
 (1)导体内P处
(1)导体内P处![]() =?
=?
过P点做以a为圆心半径为![]() 的圆周,aP与轴垂直,
的圆周,aP与轴垂直,
安培环路定律为
![]()
(取过P 点的一电力线为回路![]() )
)
可知 ![]() ,
,
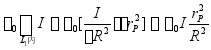
![]()
即 ![]() 。
。
方向如图所示(与轴及![]() 垂直)。
垂直)。
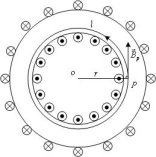
(2)导体外任一点Q处![]() =?
=?
过Q点做以O为圆心,![]() 为半径的圆周,圆周平面垂直导体轴线,安培环路定律为:
为半径的圆周,圆周平面垂直导体轴线,安培环路定律为:
![]()
 可有:
可有: ![]() ,
,![]() ,
,
![]() 。
。
![]() 方向如图所示(与轴线及
方向如图所示(与轴线及![]() 垂直)。
垂直)。
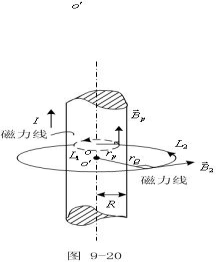
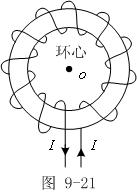
例9-10:如图所示,匀密地绕在圆环上的一组圆形
线圈,形成螺线管。设环上导线共N匝,
电流为I,求环内任一点![]() =?
=?
解:如果螺线管上导线绕的很密,则全部磁场都集中在管内,磁力线是一系列圆周,圆心都在螺线管的对称轴上。由于对称之故,在同一磁力线上各点的![]() 的大小是相同的。下面给出了螺线管过中心的剖面图。取P 所在磁力线为积分路径
的大小是相同的。下面给出了螺线管过中心的剖面图。取P 所在磁力线为积分路径![]() ,
,
![]()
可知: ![]() ,
,
![]()
即 ![]()
![]() ,方向在纸面内垂直OP. 图9-22
,方向在纸面内垂直OP. 图9-22
讨论:(1)因为r不同时,![]() 不同,所以不同半径r处
不同,所以不同半径r处![]() 大小不同。
大小不同。
(2)当L表示环形螺线管中心线的周长时,则在此圆周上各点B的大小为![]() ,
,![]() 为单位长度上的匝数。
为单位长度上的匝数。
(3)如果环外半径与内半径之差<<环中心线的半径R时,则可认为环内为均匀磁场(大小),即大小均为![]() 。
。
(4)环形螺线管中结果与无限长直螺线管中心轴线上![]() 的大小相同。
的大小相同。
与应用高斯定理求场强一样,并不能由安培环路定律求出任何情况下的磁感应强度,能够计算出![]() 的要求磁场满足它的对称性。在具有一定对称性的条件下,适选积分回路,才能计算出
的要求磁场满足它的对称性。在具有一定对称性的条件下,适选积分回路,才能计算出![]() 的值。运用安培环路定律时的程序如下:
的值。运用安培环路定律时的程序如下:
(1)分析磁场的对称性;
(2)适选闭合回路(含方向);
(3)求出![]() ,
,![]()
(4)利用![]() ,求出
,求出![]() 的值。
的值。
§9-6 带电粒子在外磁场中受力
 前面,从运动电荷在磁场中受力情况定义了
前面,从运动电荷在磁场中受力情况定义了![]() 。实验知:
。实验知:![]() 时,电荷受力
时,电荷受力![]() ;
;![]() 时,
时,![]() ,
,
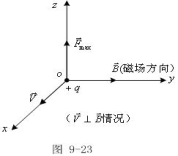
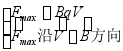 ,
,
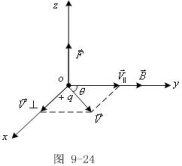
现讨论![]() 与
与![]() 夹任意角情况。如图所示,取坐标y沿
夹任意角情况。如图所示,取坐标y沿![]() 方向,
方向,![]() 在xy面内,将
在xy面内,将![]() 分解成平行于
分解成平行于![]() 及垂直于
及垂直于![]() 方向的分量
方向的分量![]() 、
、![]() ,即
,即
![]() .
.
![]() 平行于
平行于![]() 方向运动不受
方向运动不受![]() 作用,
作用,
![]()
![]() 对带电粒子作用仅是对垂直
对带电粒子作用仅是对垂直![]() 运动的作用,受力为
运动的作用,受力为

![]() (9-8)
(9-8)
说明:(1)上式叫做洛仑兹力公式。它对正、负电荷都成立。q>0,![]() 沿
沿![]() 方向;q<0,
方向;q<0,![]() 沿
沿![]() 反方向。
反方向。
(2)![]() 时,
时,![]() ;
;![]() 时,
时,![]() 。
。
(3)因为![]() ,所以,
,所以,![]() 对带电粒子不做功。
对带电粒子不做功。
(4)在均匀磁场中,![]() :做圆周运动;
:做圆周运动;![]() 与
与![]() 既不平行,也不垂直:做螺旋运动。
既不平行,也不垂直:做螺旋运动。
(5)在电磁场中运动电荷受力公式为:
![]() ,
,
即 ![]() 。
。
例9-11:用探测电荷(q>0)探测空间O点电磁场,在O处电荷速度及受力探测如下:试求:(1)O点![]() ;(2)O点
;(2)O点![]() 。
。
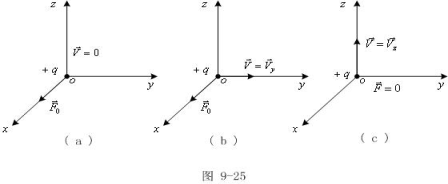
解:带电粒子在电磁场中受力为:
![]()
(1)![]() =?
=?
在(a)中,![]() ,
,![]() ,由①知:
,由①知:![]() ②
②
![]() q>0,及
q>0,及![]() 沿+x方向
沿+x方向
![]()
![]() 沿+x方向,大小为
沿+x方向,大小为![]() ③
③
(2)在(b)中,![]() ,
,![]()
![]()
![]()
![]()
![]()
在(c)中,![]() ,即
,即
![]()
![]()
![]() 沿+x方向,及
沿+x方向,及![]() ,
,![]()
![]() 沿+y方向。
沿+y方向。
![]() 的大小:
的大小:![]()
![]() ,
,
![]()
![]()
例9-12:已知某空间电磁场为![]() ,
,![]() 。一粒子q=1c,
。一粒子q=1c,![]() 在该空间运动,求
在该空间运动,求![]() =?
=?
解:

§9-7磁场对载流导体的作用
一、安培定律
实验表明,载流导体在磁场中受磁场的作用力,而磁场对载流导体的这种作用规律是安培以实验总结出来的,故该力称为安培力,该作用规律称为安培定律。
二、安培定律的数学表述
如图所示,AB为一段载流导线,横截面积为S,电流为I,电子定向运动速度为![]() ,导体放在磁场中,在C处取电流元
,导体放在磁场中,在C处取电流元![]() ,C处磁感应强度为
,C处磁感应强度为![]() ,方向向右,电流元中一个电子受洛仑兹力为
,方向向右,电流元中一个电子受洛仑兹力为
![]()
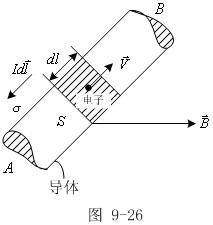 设单位体积内有n个定向运动电子,则电流元内共有运动电子数为
设单位体积内有n个定向运动电子,则电流元内共有运动电子数为![]() ,电流元中电子受合力即电流元受力为
,电流元中电子受合力即电流元受力为
 ,
,
即电流元受力
![]() (9-9)
(9-9)
此式为安培定律的数学表达式
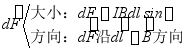
说明:(1)![]()
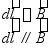 。
。
(2)对任意形状的载流导线和任意的磁场,![]() 都成立。对于一段导线受力可表示为
都成立。对于一段导线受力可表示为
![]() 。
。
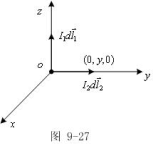
(3)如图所示,电流元![]() 位于原点,方向沿+z,
位于原点,方向沿+z,![]()
![]() 在y轴上,坐标为(0,y,0),方向沿 +y。
在y轴上,坐标为(0,y,0),方向沿 +y。![]() 在
在![]() 处产生的磁场为
处产生的磁场为
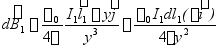 ;
;
![]() 受作用力为:
受作用力为:
![]() 。
。
![]() 在O处产生的
在O处产生的![]() ,所以
,所以![]() 受力为
受力为![]() 。
。
结论:电流元间作用力不满足牛顿第三定律。
三、计算举例
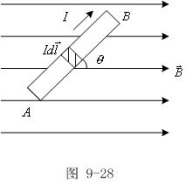
例9-13:如图所示,一段长为L的载流直导线,置于磁感应强度为![]() 的匀强磁场中,
的匀强磁场中,![]()
的方向在纸面内,电流流向与![]() 夹角为
夹角为![]() ,求导线受力
,求导线受力![]() =?
=?
解:电流元受到的安培力为
![]() ,
,
大小为 : ![]() ,
,
 方向为:垂直指向纸面。
方向为:垂直指向纸面。
![]() 导线上所有电流元受力方向相同,
导线上所有电流元受力方向相同,
![]() 整个导线受到安培力为:
整个导线受到安培力为:
![]() 可化为标量积分,
可化为标量积分,
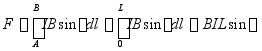 。
。
![]() 方向:垂直指向纸面。
方向:垂直指向纸面。
讨论:(1)![]() 时,
时,![]() =0。
=0。
(2)![]() 时,
时,![]() 。
。
注意:AB是闭合回路一部分,孤立的一段载流导线是不存在的。
以上是载流直导线在匀强磁场中的受力情况,一般情况下,磁场是不均匀的,这可从下面例子中看到。
例9-14:如图所示,一无限长载流直导线AB,载电流为I,在它的一侧有一长为l的有限长载流导线CD,其电流为![]() ,AB与CD共面,且
,AB与CD共面,且![]() ,C端距AB为a。求CD受到的安培力。
,C端距AB为a。求CD受到的安培力。
解:取x轴与CD重合,原点在AB上。X处电流元![]() ,在x处
,在x处![]() 方向垂直纸面向里,大小为:
方向垂直纸面向里,大小为:
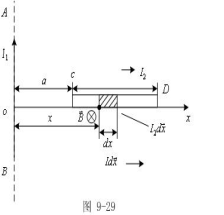
![]()
![]()
![]() ������ ������ ������ ������ ������ ������ ������ ������ ������ ������ ������ ������ ������ 方向:沿
������ ������ ������ ������ ������ ������ ������ ������ ������ ������ ������ ������ ������ 方向:沿![]() 方向。
方向。
![]() CD上各电流元受到的安培力方向相同,
CD上各电流元受到的安培力方向相同,
![]() CD段受到安培力
CD段受到安培力![]() 可化为标量
可化为标量
积分,有
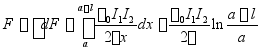
![]() 方向:沿
方向:沿![]() 方向。
方向。
注意:因为本题CD处于非均匀磁场中,所以CD受到的磁场力不能
用与磁场中的受力公式计算,即不能用![]() 计算。
计算。
以上是载流直导线在磁场中的受力情况,实际上,载流导线不
全是直的,有载流典型导线,这可以从下面例题看出。
例9-15:如图所示,半径为R、电流为I的平面载流线圈,放在匀强磁场中,磁感应强度为![]() ,
,![]() 的方向垂直纸面向外,求半圆周
的方向垂直纸面向外,求半圆周![]() 和
和![]() 受到的安培力。
受到的安培力。
解:如图所取坐标系,原点在圆心,y轴过a点,x 轴在线圈平面内。
(1)![]() 受到安培力
受到安培力![]() =?
=?
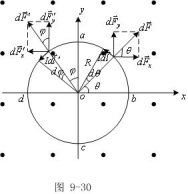 电流元
电流元![]() 受到安培力
受到安培力 ![]() ,
,
大小为 ![]() ,
,
方向为:沿半径向外。
![]()
![]() 各处电流元受力方向不同(均沿各自半径向外),
各处电流元受力方向不同(均沿各自半径向外),
将![]() 分解成
分解成![]() 及
及![]() 来进行叠加。
来进行叠加。
![]() =?
=?
![]()
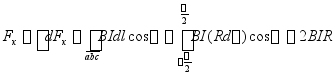 (沿+x方向)
(沿+x方向)
![]() =?
=?
![]()
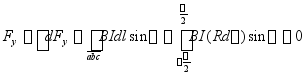
(奇函数对称区间积分为0)
实际上由受力对称性可直接得知![]() =0
=0![]() 。
。
(2)![]() =?
=?
考虑电流元![]() ,它受安培力为
,它受安培力为![]() ,大小为
,大小为![]() ,方向:沿半径向外。
,方向:沿半径向外。
![]()
![]() 上各电流元受力方向不同,
上各电流元受力方向不同,
![]() 也将
也将![]() 分解成
分解成![]() ,
,![]() 处理。
处理。
![]() ������ ������ ������ ������ ������ ������ ������ ������ ������ ������ ������ ������ ������ =?
������ ������ ������ ������ ������ ������ ������ ������ ������ ������ ������ ������ ������ =?
![]()
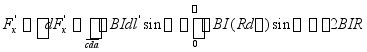 (沿-x方向)
(沿-x方向)
![]() =?
=?
![]()
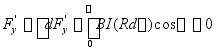
![]()
讨论:(1)各电流元受力方向不同时,应先求出![]() 及
及![]() ,之后再求
,之后再求![]() 及
及![]() 。
。
(2)分析导线受力对称性。如此题中,不用计算![]() ,
,![]() 就能知道它们为0。
就能知道它们为0。
(3)![]()
![]() ,
,![]() 圆形平面线载流线圈在均匀磁场中受力为0。
圆形平面线载流线圈在均匀磁场中受力为0。
推广:任意平面闭合线圈在均匀磁场中受安培力为0,这样,某些问题计算得到简化。
§9-8 磁场对载流线圈的作用
实验表明,当通电线圈悬挂在磁场中时,可发生旋转,这说明线圈受到了磁场对它施加力矩的作用,磁场对线圈产生的力矩称为磁力矩,下面来推导磁力矩公式。
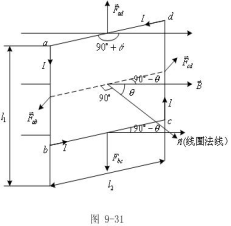 一、匀强磁场中情况
一、匀强磁场中情况
设矩形线圈边长为![]() 、
、![]() ,电流为I,
,电流为I,
线圈法向为![]() (
(![]() 与电流流向满足右手螺
与电流流向满足右手螺
旋关系),![]() 与
与![]() 夹角为
夹角为![]() ,
,![]() ,各
,各
边受力情况:
(1)![]() ,方向向上。
,方向向上。
![]() ,方向向下。
,方向向下。
可见, ![]() ,(ad,bc边受合力为0)
,(ad,bc边受合力为0)
(2)![]() ,方向:垂直纸面向外;
,方向:垂直纸面向外;
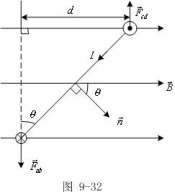
![]() ,方向:垂直纸面向里。
,方向:垂直纸面向里。
可见,ab、cd边受力形成了一力偶,力矩大小为:
![]()
力矩![]() 方向
方向![]() 方向。
方向。
定义:
![]() (9-10)
(9-10)
线圈磁矩(它只与线圈有关),由此可得出![]() 的矢量式为:
的矢量式为:
![]() (9-11)
(9-11)
 此式即为所求。
此式即为所求。
说明:(1)![]() ,大小
,大小![]() ,方向与
,方向与
线圈法向一致。
(2)对N匝线圈,![]() 。
。
(3)![]() 时,
时,![]() ,
,
![]() 时,
时,![]() 。即为平衡位置。
。即为平衡位置。
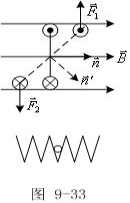
(a)![]() : 稳定平衡
: 稳定平衡
如图9-33所示,当![]() 从0有一增量时
从0有一增量时
(线圈受某种扰动),线圈位置
如虚线所示。此时线圈受到一力
 矩作用,既结果是使线圈回到平
矩作用,既结果是使线圈回到平
衡位置,所以![]() =0时称为稳定
=0时称为稳定
平衡。
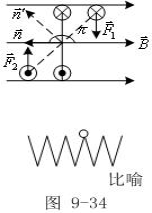
(b)![]() :不稳定平衡
:不稳定平衡
如图9-34所示,当![]() 时,线圈受
时,线圈受
某一扰动后会偏离此位置,如虚
线所示。此时线圈受到一力矩作用,
即结果是使线圈远离![]() 这一平衡位
这一平衡位
置,所以![]() 成为不稳定平衡位置。
成为不稳定平衡位置。
(4)由(3)知,线圈在磁力矩作用下,它是趋于磁通量最大位置,即![]() 方向位置。
方向位置。
(5)![]() 对任何平面线圈在匀强磁场中均成立。
对任何平面线圈在匀强磁场中均成立。
例9-16:求例10-15中线圈的![]() =?
=?![]() =?
=?
解:(1)![]() =?
=?
大小:![]() ;方向:垂直纸面向外。
;方向:垂直纸面向外。
(2)![]() =?
=?
![]() ,
,
![]()
![]() 与
与![]() 同向,
同向,![]()
![]() =0。
=0。
注意:计算![]() 时要注意下面步骤:
时要注意下面步骤:
(1)判断![]() 方向。
方向。
(2)判断![]() 与
与![]() 夹角。
夹角。
(3)找出![]() 大小,根据
大小,根据![]() 计算出
计算出![]() 大小
大小![]() 及
及![]() 的方向。
的方向。
二、非匀强磁场中情况
平面载流线圈在非匀强磁场中,一般情况下,线圈所受的合磁力及合磁力矩均不为零,此时线圈即有平动又有转动。
§9-9磁介质中的磁场
(1)与磁场有相互影响的实物物质称为磁介质,实际上一切实物都是磁介质。
(2)磁介质放在磁场中而产生磁场的状态称为磁化状态。
一、磁介质的磁化 磁导率
1、顺磁质与抗磁质的特征
空间任一点磁场是原来磁场![]() 与磁介质产生的附加磁场
与磁介质产生的附加磁场![]() 的迭加,即
的迭加,即
![]()
实验表明:如果均匀的磁介质充满有磁场的空间,则![]() 与
与![]() 同向或反向。
同向或反向。
定义:![]() 与
与![]() 同向的磁介质称为顺磁质(如:Mn,Cr,N2)
同向的磁介质称为顺磁质(如:Mn,Cr,N2)
![]() 与
与![]() 反向的磁介质称为抗介质(如:Au,Ag,Cu,H2)
反向的磁介质称为抗介质(如:Au,Ag,Cu,H2)
说明:(1)一切抗磁质和大多数顺磁质均有![]() 。
。
(2)但有为数不多的顺磁质(如:Fe,Ni)![]() ,这类磁介质称为铁磁质。
,这类磁介质称为铁磁质。
2、顺磁质及抗磁质磁化的主要机理
(1)顺磁质
分子或原子中各个电子对外界产生的磁效应的总和相当于一圆电流,该圆电流称为分子电流。它形成的磁矩称为分子磁矩![]() 。
。
组成顺磁质的分子有一定的磁矩![]() ,无
,无![]() 时(见图a),由于分子热运动,
时(见图a),由于分子热运动,![]() 方向混乱,使磁效应抵消,整个磁介质对外不显磁性。当有外磁场
方向混乱,使磁效应抵消,整个磁介质对外不显磁性。当有外磁场![]() ,每个分子磁矩都受到磁力矩作用,如图b,此力矩使分子磁矩转向
,每个分子磁矩都受到磁力矩作用,如图b,此力矩使分子磁矩转向![]() 方向,由于分子的热运动,分子磁矩尚不能与
方向,由于分子的热运动,分子磁矩尚不能与![]() 完全一致,只是在一定程度上沿外磁场方向排列起来,因而在磁介质内任一点产生与外磁场方向相同的附加磁感应强度
完全一致,只是在一定程度上沿外磁场方向排列起来,因而在磁介质内任一点产生与外磁场方向相同的附加磁感应强度![]() 如图c所示。
如图c所示。
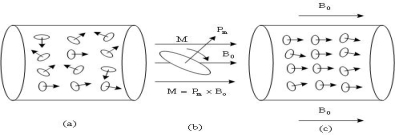
图 9-35
结论:分子磁矩是顺磁质产生磁效应的主要原因。
 (2)抗磁质
(2)抗磁质
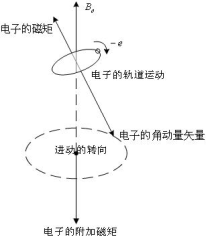
组成抗磁质的分子,在没有外磁场时,对整个分子而言,没有磁效应,它的分子电流为零。因而没有分子磁矩。当处在外磁场![]() 中时,分子或原子中的每个电子都受到洛伦兹力作用,这时电子上怎样运动的呢?可以证明:分子中每个电子在恒定的外磁场作用下除作轨道运动及自旋外,轨道平面(或角动量各量)还要以恒定的角速度绕外磁场方向转动,这种转动称为电子的进动。如下图:
中时,分子或原子中的每个电子都受到洛伦兹力作用,这时电子上怎样运动的呢?可以证明:分子中每个电子在恒定的外磁场作用下除作轨道运动及自旋外,轨道平面(或角动量各量)还要以恒定的角速度绕外磁场方向转动,这种转动称为电子的进动。如下图:
此时,电子受磁力矩![]() ,方向:
,方向:![]() 。
。
![]()
![]() ,
, ![]()
![]() 时间内:
时间内:![]() 。 图 9-36
。 图 9-36
![]() 方向
方向![]() 。
。![]() 与
与![]() 同向,
同向,![]() 与
与![]() 及
及![]() 组成的平面垂直,所以
组成的平面垂直,所以![]() 在虚线的圆周上。可见(或角动量
在虚线的圆周上。可见(或角动量![]() )绕
)绕![]() 转动。该转动称为电子进动,电子的进动亦相当一圆电流。因为电子负电,所以该圆电流的磁矩方向向下,即与
转动。该转动称为电子进动,电子的进动亦相当一圆电流。因为电子负电,所以该圆电流的磁矩方向向下,即与![]() 方向相反,分子中各个电子因进动而产生的磁效应总和亦与一圆电流等效。该圆电流产生的磁矩称为分子附加磁矩。显然,
方向相反,分子中各个电子因进动而产生的磁效应总和亦与一圆电流等效。该圆电流产生的磁矩称为分子附加磁矩。显然,![]() 方向与
方向与![]() 反向。因为
反向。因为![]() 方向都与
方向都与![]() 反向。所以在抗磁质内部任一每个分子的
反向。所以在抗磁质内部任一每个分子的![]() 与该点外磁场方向相反的附加磁场
与该点外磁场方向相反的附加磁场![]() 。可见,附加磁场
。可见,附加磁场![]() 是抗磁质产生磁效应的唯一原因。
是抗磁质产生磁效应的唯一原因。
说明:对于顺磁质也存在![]() , 分子磁矩
, 分子磁矩![]() ,且
,且![]() 。因为
。因为![]() 可忽略,故显顺磁性。所以
可忽略,故显顺磁性。所以![]() 是顺磁质产生磁效应的主要原因。对于抗磁质
是顺磁质产生磁效应的主要原因。对于抗磁质![]() , 在
, 在![]() 时,才有附加磁场
时,才有附加磁场![]() ,所以
,所以![]() 是抗磁质产生磁效应的唯一原因。
是抗磁质产生磁效应的唯一原因。
(3)磁导率
定义:![]() 称为磁介质的相对磁导率。
称为磁介质的相对磁导率。
 。
。
对一切抗磁质和大多数顺磁质,![]() ,即
,即![]()
![]()
![]() 。
。
对铁磁质:![]() 很大(
很大(![]() 比
比![]() 大得多)。
大得多)。
二、磁质中的磁场 在磁介质时的安培环路定律 磁场强度
1、回顾
真空中 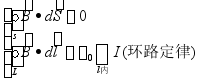
若放入磁介质中,上面二式如何?
因为,磁力线是闭合的,所以 ![]() 成立。环路定律形式如何?后面讨论。
成立。环路定律形式如何?后面讨论。
2、有磁介质时安培环路定律
传导电流:导体中电子,或正、负离子作有规则运动形成的电流。
因为磁现象的根源是电流,所以安培环路中![]() 应是传导电流
应是传导电流![]() 与分子电流
与分子电流![]() 的总和,即
的总和,即
![]()
![]() (“+”顺磁质,“-”抗磁质)
(“+”顺磁质,“-”抗磁质)

![]()
![]()
![]()
![]() (9-12)
(9-12)
称为磁介质的磁导率。顺磁质:![]() ;抗磁质:
;抗磁质:![]() ;铁磁质:
;铁磁质:![]() 比
比![]() 大得多。
大得多。
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]() “+”顺磁质,“-”抗磁质
“+”顺磁质,“-”抗磁质
取回路abcd,ab在螺线管内,cd在外。
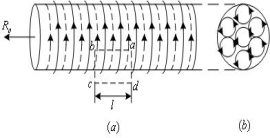 可知
可知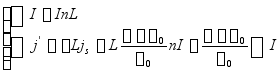
![]()
![]()
![]()
![]()
![]() , (9-13) 图9-37
, (9-13) 图9-37
![]() (9-14)
(9-14)
式(9-13)为磁介质中的安培环路定律(此积分仅与传导电流有关),式(9-14)中的![]() 称为磁场强度。
称为磁场强度。
说明:(1)上式是从螺线管中导出的,但普遍成立。
(2) ![]() 为辅助量,无直接的物理意义,有意义的是
为辅助量,无直接的物理意义,有意义的是![]() 。
。
 (3)安培环路定律
(3)安培环路定律![]() 利用与真空中
利用与真空中![]() 实验一样,求
实验一样,求![]() 时,先求
时,先求![]() ,后求
,后求![]() 。
。
三、铁磁质简介
铁磁质的性质和规律比顺磁质、抗磁质复
杂,下面通过研究![]() ,
,![]() 关系的实验来做一些简
关系的实验来做一些简
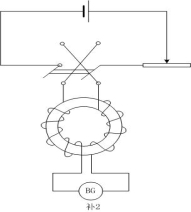
单介绍。实验是用图9- 所示的电路来进行的。
把待测的铁磁质做成圆环,在圆环上密绕线圈,
这样就形成以铁磁质为芯的环形螺线管。线圈通
电时,环内磁场强度为
![]() 图 9-38
图 9-38
圆环内的![]() ,可用一个接在冲击电流计
,可用一个接在冲击电流计![]() 上副线圈来测量。当原线圈(即环形螺线管)
上副线圈来测量。当原线圈(即环形螺线管)
 中电流变化甚至反向时,在副线圈中将产生一个
中电流变化甚至反向时,在副线圈中将产生一个
感应电动势,由此可把环内的![]() 测出来。实验结
测出来。实验结
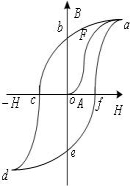
果得到如图的![]() 曲线。
曲线。
![]() 称为起始磁化曲线,当
称为起始磁化曲线,当![]() 从零逐渐增加
从零逐渐增加
时,![]() 亦从零增加,当
亦从零增加,当![]() 增大到一定值时(图
增大到一定值时(图
中![]() 点),
点),![]() 几乎不再增加,这时磁化达到了饱和。
几乎不再增加,这时磁化达到了饱和。
由于磁化曲线不是直线,所以铁磁质的磁导
率![]() 以及相对磁导率
以及相对磁导率![]() 都不是恒量。
都不是恒量。
在磁化达到不饱和后,令![]() 减小,则
减小,则![]() 亦减小, 图 9-39
亦减小, 图 9-39
但不按![]() 减小,而是沿曲线
减小,而是沿曲线![]() 减小,当
减小,当![]() 等于
等于
零时,![]() ,即磁化场减小到零时,介质的磁
,即磁化场减小到零时,介质的磁
化状态并不恢复到原来的起点![]() ,而是保留一定
,而是保留一定
的磁性,叫剩磁现象,![]() 叫剩余磁感应强度。如果
叫剩余磁感应强度。如果![]() 的值等于
的值等于![]() 值,
值,![]() 变为零,即介质完全退磁,使介质完全退磁所需的反向磁场强度
变为零,即介质完全退磁,使介质完全退磁所需的反向磁场强度![]() 叫做矫顽力。当反向磁场
叫做矫顽力。当反向磁场![]() 继续增加时,铁磁质将向反方向磁化,达到饱和后,若使反向磁场
继续增加时,铁磁质将向反方向磁化,达到饱和后,若使反向磁场![]() 的减小到零,然后再向正方向增加,
的减小到零,然后再向正方向增加,![]() 将沿
将沿![]() 曲线而变化,形成闭合曲线
曲线而变化,形成闭合曲线![]() 。曲线
。曲线![]() 称为磁滞回线。各种铁磁性材料有不同的磁滞回线。他们的区别在于矫顽力的大小不同。铁磁材料按矫顽力的大小分为两类,即硬磁材料和软磁材料。
称为磁滞回线。各种铁磁性材料有不同的磁滞回线。他们的区别在于矫顽力的大小不同。铁磁材料按矫顽力的大小分为两类,即硬磁材料和软磁材料。
1