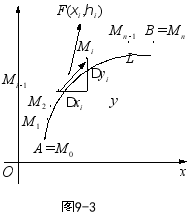日期：2020.

专业：

姓名：

一、学习指南

1.课题名称：

常数项级数的概念和性质

2.达成目标：

（1）能从无穷数列出发掌握常数项无穷级数的定义（难度：★)．

（2）利用前n项和与极限熟练掌握常数项级数的收敛、发散概念（难度：★★)．

（3）记忆并理解常数项级数的性质（难度：★★★)．

（4）能利用定义具体判断给定级数的敛散性，并能把几类特殊级数作为结论记住。（难度：★★★)．

3.学习方法建议：

（1）观看微课视频、查找资料法．

（https://www.bilibili.com/video/av19027609/?spm_id_from=333.788.videocard.1）

（2）成立自主学习小组3-5人，讨论为主．

（3）教师在线答疑．

4.课堂学习形式预告：

一、交流自主学习成果．

二、例题及习题自主完成．

三、展示质疑，全班讨论．

二、学习任务

1、常数项级数的概念．

2、常数项级数的表示方法．

3、常数项级数收敛、发散的定义．

4、余和（余项）的定义

5、思考：生活中寻找蕴含常数项级数的实例，并分组讨论收敛及发散．

1、几何级数（等比级数）的敛散性．

2、掌握级数通项乘法变差，相互抵消的题型．

注意：这是一种类型，尝试探讨总结规律．

1、无穷项级数的性质（用定义理解）．

2、收敛级数的必要条件的逆否命题很重要．

3、例题讲解．

4、自主练习或讨论

例： 讨论级数的敛散性．

三、困惑与建议

日期：2020

专业：

姓名：

一、学习指南

1.课题名称：

正项级数

2.达成目标：

（1）掌握正项级数的定义（难度：★).

（2）正项级数收敛的判别法。（难度：★★★).

  部分和数列有界；比较审敛法；比较审敛法的极限形式；比值审敛法；根值审敛法

注意事项：不同判别法有各自相对使用的题型，这种判断能力建立在一定计算题量基础上.

3.学习方法建议：

（1）观看微课视频、查找资料法（https://www.bilibili.com/video/av19027609/?spm_id_from=333.788.videocard.1）

（2）成立自主学习小组3-5人，讨论为主。

（3）教师在线答疑。

4.课堂学习形式预告：

一、交流自主学习成果。

二、例题及习题自主完成。

三、展示质疑，全班讨论。

二、学习任务

1、正项级数的定义.

2、正项级数判别法，部分和数列有界.

    3、P级数的收敛性判别.

1、比值审敛法

注意：找通项，求极限，判断极限值与去的关系。

2、根值审敛法

注意：通项通常带有n次幂

3、比较判别法.

注意：这个方法的关键是寻找已知级数作为比较对象，所以强调一些特殊级数敛散性的记忆。

4、积分判别法可自主选学

     1、积分判别法例题讲解，题目特别好！

三、困惑与建议

日期：2020.

专业：

姓名：

一、学习指南

1.课题名称：

 一般项级数及其审敛法

2.达成目标：

（1）交错级数定义（难度：★).

（2）掌握交错级数的莱布尼兹定理（难度：★★).

（3）了解无穷级数绝对收敛与条件收敛的概念及关系。（难度：★★★).

（4）会判别一般项级数的敛散性习题（难度：★★★).

3.学习方法建议：

（1）观看微课视频、查找资料法（https://www.bilibili.com/video/av19027609/?spm_id_from=333.788.videocard.1）

（2）成立自主学习小组3-5人，讨论为主.

（3）教师在线答疑.

4.课堂学习形式预告：

一、交流自主学习成果．

二、例题及习题自主完成．

三、展示质疑，全班讨论．

二、学习任务

1、交错级数定义。

2、莱布尼兹定理

    注意：定理中是（1）（）；（2）

3、绝对收敛与条件收敛．

如果级数收敛，则级数收敛．

4、例题讲解．

5、自主总结绝对收敛和条件收敛的差别

6、练习：

（1）;     （2）;     （3）;  

三、困惑与建议

日期：2020

专业：

姓名：

一、学习指南

1.课题名称：

幂级数

2.达成目标：

（1）掌握数项级数的概念（难度：★★).

（2）掌握幂级数的定义，求幂级数的收敛半径、收敛区间及收敛域的方法。（难度：★★★).

（3）学习幂级数及其收敛区间内的一些基本性质，会求一些幂级数在收敛区间内的和函数，并会由此求出某些级数的和（难度：★★★).

3.学习方法建议：

（1）观看微课视频、查找资料法（https://www.bilibili.com/video/av19027609/?spm_id_from=333.788.videocard.1）

（2）成立自主学习小组3-5人，讨论为主.

（3）教师在线答疑.

4.课堂学习形式预告：

一、交流自主学习成果．

二、例题及习题自主完成．

三、展示质疑，全班讨论．

二、学习任务

1、数项级数定义.

2、数项级数的收敛点，收敛域.

3、例题讲解：几何级数

方法：利用数项级数的结论

1、幂级数定义．

2、幂级数收敛域的三种情况.

3、幂级数收敛半径的求法。

4、例题讲解

学习方法：多思考，多练习，多讨论，小组学习，取长补短

三、困惑与建议

日期：2020.

专业：

姓名：

一、学习指南

1.课题名称：

函数展开成幂级数

2.达成目标：

（1）掌握函数展开成泰勒级数的定理及步骤（难度：★★★).

（2）麦克劳林级数（难度：★★★).

（3）函数展开成幂级数的方法（难度：★★★).

（4）

3.学习方法建议：

（1）观看微课视频、查找资料法（https://www.bilibili.com/video/av19027609/?spm_id_from=333.788.videocard.1）

（2）成立自主学习小组3-5人，讨论为主.

（3）教师在线答疑.

4.课堂学习形式预告：

一、交流自主学习成果．

二、例题及习题自主完成．

三、展示质疑，全班讨论．

二、学习任务

1、函数展成泰勒级数

2、展开式的系数表达式及表达式唯一

1、记忆常用初等函数的幂级数．

    注意：取值范围

2、余项极限为零是关键．

3、间接展开法．

4、例题讲解

学习方法：熟记公式，打好基础，不能着急

1、例题

2、一些特殊级数可推导出一些常见数项级数的和

三、困惑与建议

日期：

专业：

姓名：

一、学习指南

1.课题名称：

函数的幂级数展开式的应用

2.达成目标：

（1）掌握幂级数在实际中的一些近似应用（难度：★★★).

（2）了解欧拉公式（难度：★★).

3.学习方法建议：

（1）观看微课视频、查找资料法（https://www.bilibili.com/video/av19027609/?spm_id_from=333.788.videocard.1）

（2）成立自主学习小组3-5人，讨论为主.

（3）教师在线答疑.

4.课堂学习形式预告：

一、交流自主学习成果．

二、例题及习题自主完成．

三、展示质疑，全班讨论．

二、学习任务

1、通过展开式计算一些计算值

例1  计算的近似值，使误差不超过．

2、计算没有初等函数作为原函数的积分

例2  求的近似值，精确到（取）

1、欧拉公式

2、分组讨论数学的美

三、困惑与建议

日期：2020.

专业：

姓名：

一、学习指南

1.课题名称：

傅里叶级数

2.达成目标：

（1）掌握傅里叶级数的概念（难度：★★).

（2）掌握函数展成傅里叶级数的收敛定理（难度：★★★).

（3）会将函数展成傅里叶级数（难度：★★★).

（4）会将定义在[-L，L]上的函数展开为傅里叶级数（难度：★★★).

（5）会将定义在[0，L]上的函数展开为正弦级数与余弦级数（难度：★★★).

3.学习方法建议：

（1）观看微课视频、查找资料法（https://www.bilibili.com/video/av19027609/?spm_id_from=333.788.videocard.1）

（2）成立自主学习小组3-5人，讨论为主.

（3）教师在线答疑.

4.课堂学习形式预告：

一、交流自主学习成果．

二、例题及习题自主完成．

三、展示质疑，全班讨论．

二、学习任务

1、三角函数系及其正交性

2、三角级数

3、傅里叶级数及其收敛性

4、具体展开时重点为计算傅里叶系数

注意：积分是关键，分部积分

5、收敛定理

    6、例题讲解

.

1、正弦级数和余弦级数：

一般来说，一个函数的傅立叶级数既含有正弦项，又含有余弦项，但是也有一些函数的傅立叶级数只含正弦项或只含有常数项和余弦项．如果只含正弦项，即，则称

为正弦级数；如果不含正弦项，即，则称

为余弦级数.

2、在[-L，L]的函数展开

三、困惑与建议

日期：2020

专业：机械

姓名：

一、学习指南

1.课题名称：

第二类曲线积分

2. 达成目标：

（1）理解变力在曲线上的功（难度：★★).

（2）掌握第二类曲线积分的定义（难度：★★).

（3）会求第二类曲线积分的例题（难度：★★★).

（4）能区分两类曲线积分的联系与不同（难度：★★★).

3.学习方法建议：

（1）观看微课视频、查找资料法（https://www.bilibili.com/video/av19027609/?spm_id_from=333.788.videocard.1）

（2）成立自主学习小组3-5人，讨论为主.

（3）教师在线答疑.

4.课堂学习形式预告：

一、交流自主学习成果．

二、例题及习题自主完成．

三、展示质疑，全班讨论．

二、学习任务

1、物理问题分析．

在物理学中还遇到另一种类型的曲线积分问题.例如,一个质点在面内受到力

 ij

的作用，从点沿光滑曲线弧移动到点，求力所作的功

（图93）.

     要求：能分组描述出功的求解思路

2、第二类曲面积分定义

 要求：记忆

.     

.

类似地，把

3、对比掌握曲线积分性质

4、两类积分之间的关系

1、第二类曲线积分的计算

2、例题讲解．

三、困惑与建议

日期：2020.

专业：

姓名：

一、学习指南

1.课题名称：

格林公式（1）

2.达成目标：

（1）掌握格林公式（难度：★★).

（2）利用格林公式计算题目（难度：★★★).

3.学习方法建议：

（1）观看微课视频、查找资料法（https://www.bilibili.com/video/av19027609/?spm_id_from=333.788.videocard.1）

（2）成立自主学习小组3-5人，讨论为主.

（3）教师在线答疑.

4.课堂学习形式预告：

一、交流自主学习成果．

二、例题及习题自主完成．

三、展示质疑，全班讨论．

二、学习任务

1、连通区域．

单连通、复连通

2、区域的正方向．

3、记忆格林公式的要求

1、格林公式推导证明过程．

方法：分区域利用格林，复杂图形类似中学添加辅助线

2、例题讲解

注意：不封闭区域要先变为封闭区域

三、困惑与建议

日期：2020.

专业：

姓名：

一、学习指南

1.课题名称：

格林公式（2）

2.达成目标：

（1）掌握积分与路径无关的四个互相等价结论（难度：★★★).

（2）会求函数的全微分（难度：★★★).

3.学习方法建议：

（1）观看微课视频、查找资料法（https://www.bilibili.com/video/av19027609/?spm_id_from=333.788.videocard.1）

（2）成立自主学习小组3-5人，讨论为主.

（3）教师在线答疑.

4.课堂学习形式预告：

一、交流自主学习成果．

二、例题及习题自主完成．

三、展示质疑，全班讨论．

二、学习任务

1、积分与路径无关．

通过具体习题引入问题，寻找条件

2、记忆四个等价条件．

1、四个等价条件的证明．

三、困惑与建议

日期：2020.

专业：

姓名：

一、学习指南

1.课题名称：

第一类曲面积分

2.达成目标：

（1）掌握第一类曲面积分的概念（难度：★★).

（2）会计算第一类曲面积分的题目（难度：★★★).

3.学习方法建议：

（1）观看微课视频、查找资料法（https://www.bilibili.com/video/av19027609/?spm_id_from=333.788.videocard.1）

（2）成立自主学习小组3-5人，讨论为主.

（3）教师在线答疑.

4.课堂学习形式预告：

一、交流自主学习成果．

二、例题及习题自主完成．

三、展示质疑，全班讨论．

二、学习任务

2、第一类曲面积分的定义．

2、曲面积分性质自己课下分组讨论．

3、偏导与连续的关系

3、第一类曲面积分的计算．

 .

2、曲面的参数方程形式，根据个人能力自主学习．

3、例题讲解

方法：多思考

三、困惑与建议

日期：2020.

专业：

姓名：

一、学习指南

1.课题名称：

第二类曲面积分

2.达成目标：

（1）双侧曲面的定义（难度：★★).

（2）掌握第二类曲面积分的概念（难度：★★).

（3）会计算第二类曲面积分的题目（难度：★★★).

3.学习方法建议：

（1）观看微课视频、查找资料法（https://www.bilibili.com/video/av19027609/?spm_id_from=333.788.videocard.1）

（2）成立自主学习小组3-5人，讨论为主.

（3）教师在线答疑.

4.课堂学习形式预告：

一、交流自主学习成果．

二、例题及习题自主完成．

三、展示质疑，全班讨论．

二、学习任务

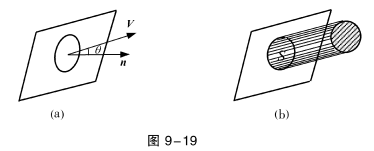
3、曲面的侧：前后、左右、上下、内外

实践 ：通过莫比乌斯带理解

2、引例讲解

在物理学中,会遇到如何计算流向曲面一侧的流量的问题.例如,设稳定流动（即流速与时间无关）的不可压缩流体（假定密度为1）的速度场由

ijk

给出，是速度场中的一片有向曲面，函数，，都在上连续，求在单位时间内流向指定一侧的流体的质量，即流量.

3、第二类曲面积分的定义．

4、曲线积分的性质

作业：对照第二类曲线积分，找到性质有差异的地方

4、第二类曲面积分的计算．

.

2、例题讲解

方法：多思考

三、困惑与建议

日期：2020.

专业：

姓名：

一、学习指南

1.课题名称：

高斯公式与斯托克斯公式

2.达成目标：

（1）掌握高斯公式的结论（难度：★★).

（2）利用高斯公式计算例题（难度：★★★).

（3）掌握斯托克斯公式的结论（难度：★★).

（4）利用斯托克斯公式计算例题（难度：★★★).

3.学习方法建议：

（1）观看微课视频、查找资料法（https://www.bilibili.com/video/av19027609/?spm_id_from=333.788.videocard.1）

（2）成立自主学习小组3-5人，讨论为主.

（3）教师在线答疑.

4.课堂学习形式预告：

一、交流自主学习成果．

二、例题及习题自主完成．

三、展示质疑，全班讨论．

二、学习任务

1、熟记高斯公式

,                 （）

注意：按格林公式推广理解．

2、高斯公式证明

3、高斯简介---精神食粮

1、例题讲解．

    注意：应用条件必须满足

三、困惑与建议