一 实验目的
随着信息技术的发展,数字化时代已经到来,数字信号的处理逐步发展成为一门主流技术。滤波技术的发展,对信息处理技术的发展具有及其重要的作用,相对于模拟滤波器,数字滤波器没有漂移,能够处理低频信号,频率响应特性可做成非常接近于理想的特性,且精度可以达到很高,容易集成等这些优势决定了数字滤波器的应用越来越广泛,同时DSP数字信号处理器的出现也促进了数字滤波器的发展。
本实验学习IIR数字滤波器的设计原理及其在DSP上的实现思路并对用DSP实现IIR滤波器的方法进行了分析。用MATLAB计算出IIR数字滤波器的系数,产生输入数据,应用CCS软件调试汇编程序,并用TMS320C54为设置参数使用CCS对IIR进行了仿真。
1.加深对IIR滤波器原理和基本性质的理解;
2.熟悉IIR滤波器设计流程和应用;
3.学习DSP中IIR滤波器的设计和编程思想;
4.学习使用CCS的波形观察窗口观察信号波形和频谱情况。
5.进一步熟悉CCS的各种基本操作
二 使用仿真工具的介绍
2.1 MATLAB的介绍
本设计中应用M文件设计IIR滤波器的参数,所以在本课程设计中有必要对MATLAB进行简要的描述。
MATLAB语言是当今国际上科学界最具影响力、也是最具活力的软件。它具有强大的数学运算能力、方便实用的绘图功能及语言的高度集成性。MATLAB是矩阵实验室之意。MATLAB除具备卓越的数值计算能力外,它还提供了专业水平的符号计算、文字处理、可视化建模仿真和实时控制等功能。
MATLAB的出现使得通信系统的仿真能够用计算机模拟实现,免去构建实验系统的不便,而且操作十分简便,只需要输入不同的参数就能得到不同情况下系统的性能,而且在结果的预测和数据的存储方面也比传统的方式有很多优势。因而MATLAB在通信仿真邻域得到越来越多的应用。MATLAB的一大特点是提供了很多专用的工具箱和模块库,例如通信工具箱和模块库‘数字信号处理工具箱和模块库、控制工具箱和模块库等,MATLAB在这些工具箱和模块库中提供了很多常用的函数和模块,使得仿真更容易实现。
2.2 CCS的介绍
CCS的全称是Code Composer Studio,它是美国德州仪器公司(Texas Instrument, TI)出品的代码开发和调试套件。TI公司的产品线中有一大块业务是数字信号处理器(DSP)和微处理器(MCU),CCS便是供用户开发和调试DSP和MCU程序的集成开发软件。
CCS是一种针对TMS320系列DSP的集成开发环境,在Windows操作系统下,采用图形接口界面,提供有环境配置、源文件编辑、程序调试、跟踪和分析等工具。
CCS有两种工作模式,即 :
软件仿真器模式:可以脱离DSP芯片,在PC机上模拟DSP的指令集和工作机制,主要用于前期算法实现和调试。
硬件在线编程模式:可以实时运行在DSP芯片上,与硬件开发板相结合在线编程和调试应用程序。
CCS的开发系统主要由以下组件构成:
① TMS320C54x集成代码产生工具;
② CCS集成开发环境;
③ DSP/BIOS实时内核插件及其应用程序接口API;
④ 实时数据交换的RTDX插件以及相应的程序接口API;
⑤ 由TI公司以外的第三方提供的各种应用模块插件。
CCS的功能十分强大,它集成了代码的编辑、编译、链接和调试等诸多功能,而且支持C/C++和汇编的混合编程,其主要功能如下:
① 具有集成可视化代码编辑界面,用户可通过其界面直接编写C、汇编、.cmd文件等;
② 含有集成代码生成工具,包括汇编器、优化C编译器、链接器等,将代码的编辑、编译、链接和调试等诸多功能集成到一个软件环境中;
③ 高性能编辑器支持汇编文件的动态语法加亮显示,使用户很容易阅读代码,发现语法错误;
④ 工程项目管理工具可对用户程序实行项目管理。在生成目标程序和程序库的过程中,建立不同程序的跟踪信息,通过跟踪信息对不同的程序进行分类管理;
⑤ 基本调试工具具有装入执行代码、查看寄存器、存储器、反汇编、变量窗口等功能,并支持C源代码级调试;
⑥ 断点工具,能在调试程序的过程中,完成硬件断点、软件断点和条件断点的设置;
⑦ 探测点工具,可用于算法的仿真,数据的实时监视等;
⑧ 分析工具,包括模拟器和仿真器分析,可用于模拟和监视硬件的功能、评价代码执行的时钟;
⑨ 数据的图形显示工具,可以将运算结果用图形显示,包括显示时域/频域波形、眼图、星座图、图像等,并能进行自动刷新;
⑩ 提供GEL工具。利用GEL扩展语言,用户可以编写自己的控制面板/菜单,设置GEL菜单选项,方便直观地修改变量,配置参数等;
三 实验原理
数字滤波器可以理解为是一个计算程序或算法,将代表输入信号的数字时间序列转化为代表输出信号的数字时间序列,并在转化过程中使信号按预定的形式变化。数字滤波器有多种分类,按频率特性可划分为低通数字滤波器、高通数字滤波器、带通数字滤波器、带阻数字滤波器。根据数字滤波器冲激响应的时域特征,可分为无限长冲激响应(IIR)滤波器和有限长冲激响应(FIR)滤波器。
3.1 IIR数字滤波器的基本概念
无限脉冲响应滤波器是数字滤波器的一种简称IIR数位滤波器(infinite impulse response filter)。由于无限脉冲响应滤波器中存在反馈回路,因此对于脉冲输入信号的响应是无限延续的。IIR滤波器有以下几个特点:
1、IIR数字滤波器的系统函数可以写成封闭函数的形式。
2、IIR数字滤波器采用递归型结构,即结构上带有反馈环路。IIR滤波器运算结构通常由延时、乘以系数和相加等基本运算组成,可以组合成直接型、正准型、级联型、并联型四种结构形式,都具有反馈回路。由于运算中的舍入处理,使误差不断累积,有时会产生微弱的寄生振荡。
3、IIR数字滤波器在计上可以借助成熟的模拟滤波器的成果,如巴特沃斯、契比雪夫和椭圆滤波器等,有现成的设计数据或图表可查,其设计工作量比较小,对计算工具的要求不高。在设计一个IIR数字滤波器时,我们根据指标先写出模拟滤波器的公式,然后通过一定的变换将模拟滤波器的公式转换成数字滤波器的公式。
4、IIR数字滤波器的相位特性不好控制,对相位要求较高时,需加相位校准络。
5、IIR单位响应为无限脉冲序列FIR单位响应为有限的。
6、IIR幅频特性精度很高,不是线性相位的,可以应用于对相位信息不敏感的音频信号上。FIR幅频特性精度较之于IIR低,但是线性相位就是不同频率分量的信号经过FIR滤波器后他们的时间差不变。这是很好的性质。
3.2无限脉冲响应滤波器的缺点:
1、脉冲响应为无限长,造成当输入数位讯号为有限长的时候输出数位讯号会变成无限长。
2、比有限脉冲响应滤波器较不易最佳化。
3、不一定是稳定的因为Z转换后所有的极点不一定都在单位圆内。
3.3 IIR滤波器的结构和基本表达:
IIR数字滤波器的单位脉冲响应h(n)是无限长的,结构上有输出到输入的反馈,频率采样结构除外是递归型。
IIR滤波器差分方程的一般表达式为:
![]() 2-1
2-1
式中x(n)为输入序列;y(n)为输出序列;和为滤波器系数.若所有系数等于0,则为FIR滤波器.
IIR滤波器具有无限长的单位脉冲响应,在结构上存在反馈回路,具有递归性,即IIR滤波器的输出不仅与输入有关,而且与过去的输出有关.
将上式展开得出y(n)表达式为:
![]()
2-2
在零初始条件下,对上式进行z变换,得到:
![]()
2-3
设N=M,则传递函数为:
![]() 2-4
2-4
上式可写成 :
![]() 2-5
2-5
上式具有N个零点和N个极点.若有极点位于单位圆外将导致系统不稳定.由于FIR滤波器所有的系数均为0,不存在极点,不会造成系数的不稳定.对于IIR滤波器,系统稳定的条件如下:
若||<1,当n→时,h(n)→0,系统稳定;
若||>1,当n→时,h(n)→,系统不稳定.
IIR滤波器具有多种形式,主要有:直接型(也称直接I型)、标准型(也称直接II型)、变换型、级联型和并联型.
二阶IIR滤波器,又称为二阶基本节,分为直接型、标准型和变换型.
对于一个二阶IIR滤波器,其输出可以写成:
![]()
在二阶IIR滤波器结构中,标准型结构是最常见的滤波器结构,其结构如图1所示:
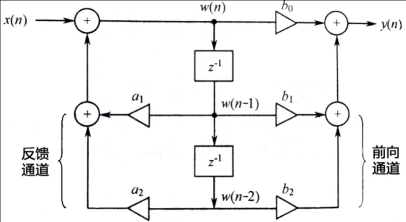
图1 标准型结构
由以上两式对二阶IIR滤波器进行编程,其中乘法-累加运算可采用单操作数指令或双操作数指令,数据和系数可存放在DARAM中,如图2所示:
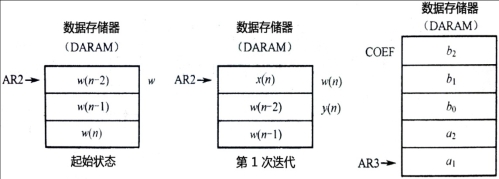
为了实现直接型滤波,可在DARAM中开辟4个循环缓冲区,用来存放变量和系数,并采用循环缓冲区方式寻址.这4个循环缓冲区的结构如图3所示:
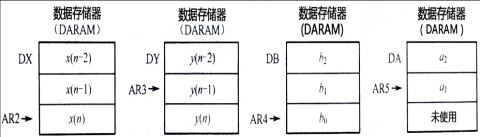
图3 循环缓冲区结构
(程序中为x_data、y_data、b_coef 、a_coef)
四 实验内容
4.1 实验步骤
1.利用MATLAB来确定IIR滤波器的参数;
2.启动CCS,在CCS中建立一个汇编源文件、和一个命令文件,并将这两个文件添加到工程,再编译并装载程序;
3.设置时域观察窗口,得到其滤波前后波形变化图;
4.设置频域观察窗口,得到其滤波前后频谱变化图.
4.2利用MATLAB计算滤波器系数
参考教材174页的设计过程,根据输入数据的频域特性,确定截止频率为0.2,纹波3dB,采用直接型II阶,输入如下MATLAB语句
[b,a]=cheby1(2,3,100/500)
freqz(b,a,512,1000)
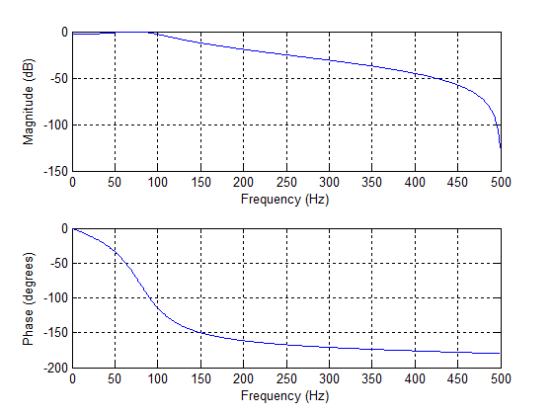
为了获得归一化的整数参数,输入如下语句完成参数的归一化
round(b*32768/10)
ans =
135 270 135
>> round(a*32768/10)
ans =
3277 -4722 2208
由于程序中a0默认已经存在,所以实际上只需要输入b0、b1、b2、a1、a2。
4.3汇编语言程序
程序主体由iir3、main、vector三个子程序组成。
main:主调用子程序,用来调用其他子程序,实现统一的接口。
vector:实现中断。
iir3:IIR算法子程序。
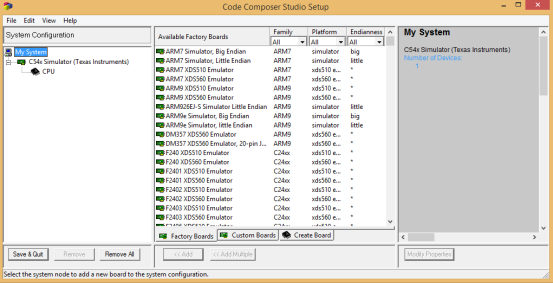
点击左侧C54 Simulator观察仿真器是否选择正确
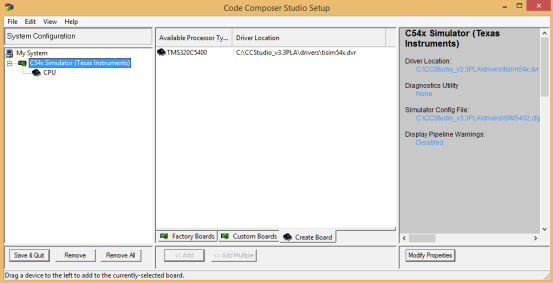
如不正确,返回选择C5402 Simulator。
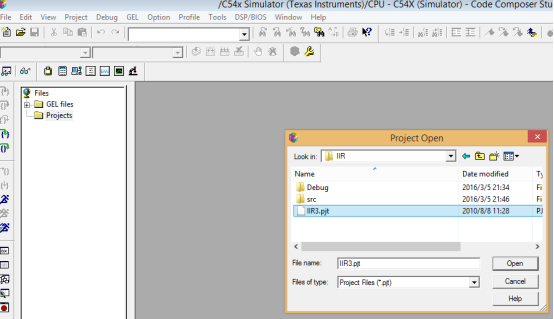
2.双击图标 启动ccs3.3,如下图选择Project->Open
启动ccs3.3,如下图选择Project->Open
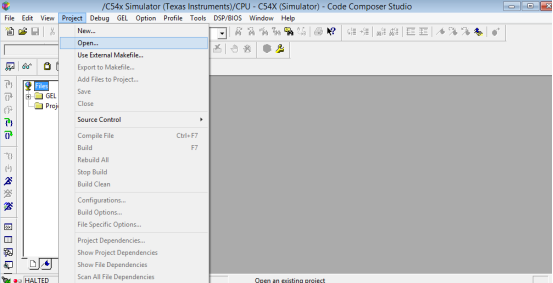
3.找到安装目录,选择项目文件DSPfft,点击Open
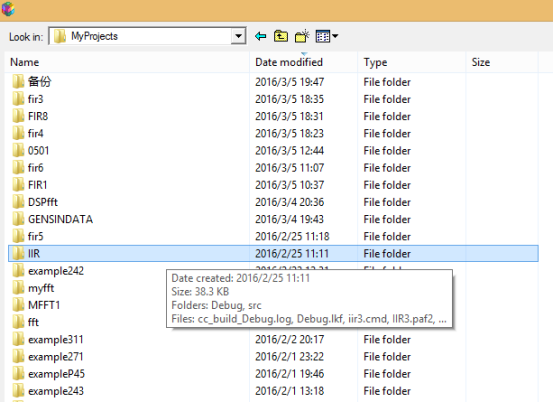
选择iir3.pjt,点击Open
点击IIR3.pjt前的加号

4.双击iir3.asm,阅读滤波器程序源代码,找出输入数据input,输出数据output, 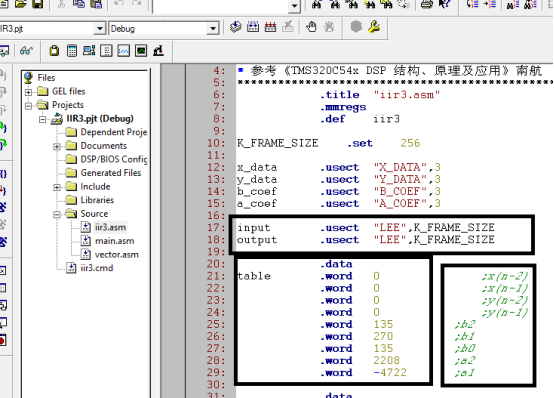
5. 根据MATLAB的滤波器参数计算结果修改滤波器参数如上图,注意只需要输入b0、b1、b2、a1、a2。
6.依次点击从左到右的三个按钮,完成编译和链接等步骤。

7.加载out文件,如图所示
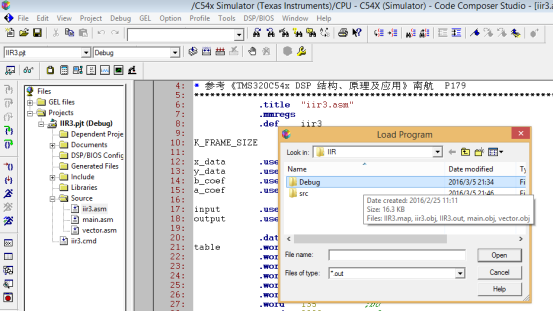
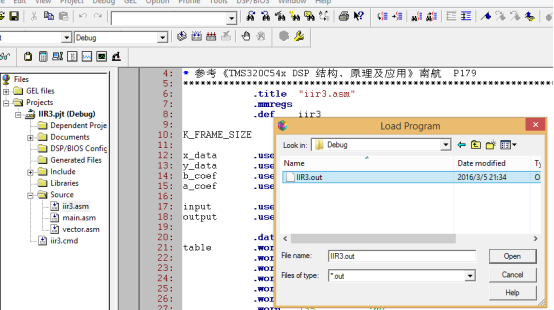
出现黄色小箭头表明加载成功
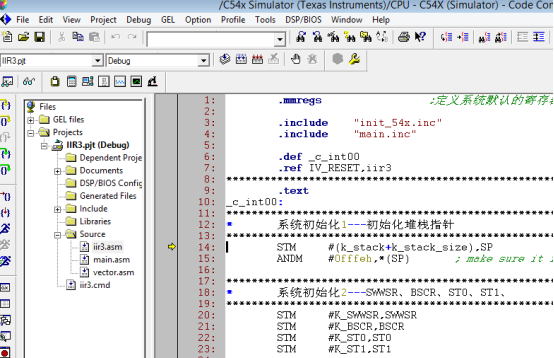
8.运行程序,点击最右侧上方的跑步小人按钮,大约3到5秒钟后点击下方的停止运行按钮(左侧有X的跑步小人)。

9.观察输入输出波形,点击上方菜单view->graph->time/frequency
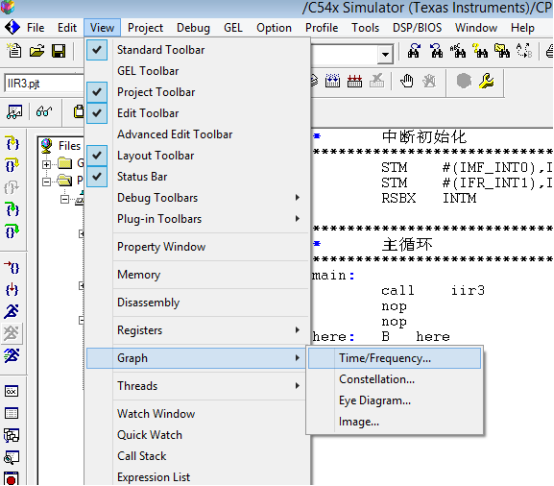
依照图中配置参数,先点击Single Time下拉菜单修改为如图的FFT Magnitude
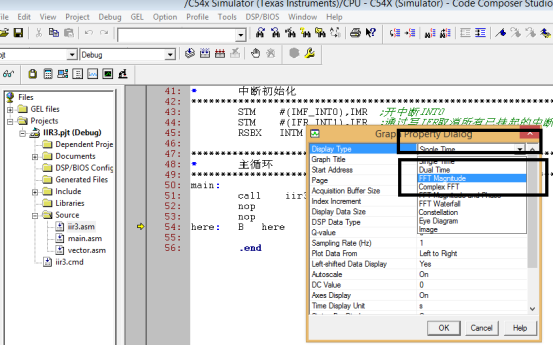
input是点击后手动输入,其他参数如下图配置
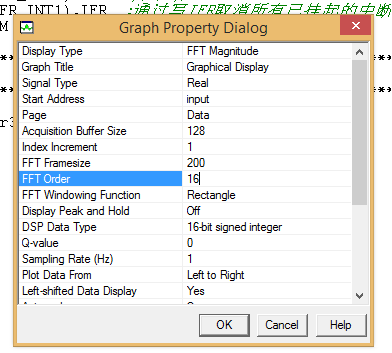
点击OK,观察输入波形
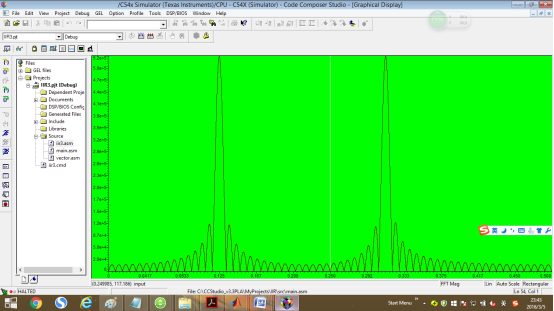
关掉波形(下面的小X),再次点击上方菜单view->graph->time/frequency,将观察变量改为output,如图配置,观察输出图形(频域)
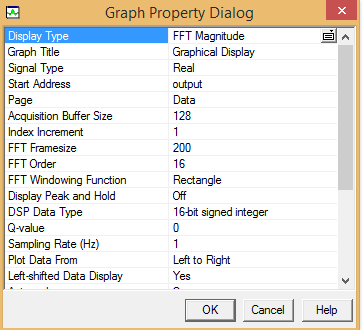
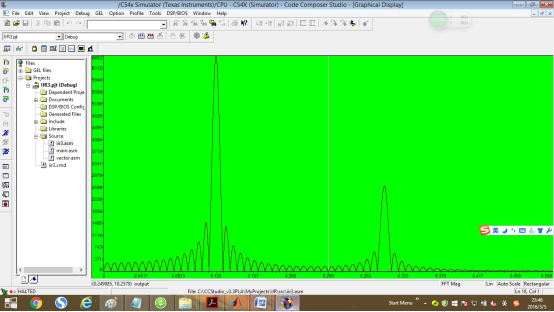
进一步思考:为什么二阶的IIR滤波器滤波效果不如高阶滤波器好(包括高阶FIR和IIR滤波器,例如16阶FIR滤波器),不能完全消除右边的频谱峰值?
10.可以重新设计滤波器参数,改变滤波器参数配置可以再做次实验。
注意每次修改源代码后均要重复编译链接和加载out文件、运行、停止等过程。
![]()
