第三部分   扭转

4.1预备知识

一、基本概念

1、扭转变形

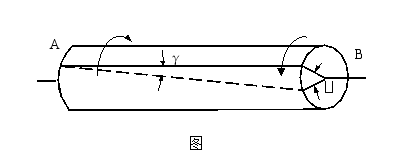
扭转变形是杆件的基本变形之一，扭转变形的受力特点是：杆件受力偶系的作用，这些力偶的作用面都垂直于杆轴。此时，截面B相对于截面A转了一个角度，称为扭转角。同时，杆件表面的纵向直线也转了一个角度变为螺旋线，称为剪切角。

2、外力偶

杆件所受外力偶的大小一般不是直接给出时，应经过适当的换算。若己知轴传递的功率P(kW)和转速n(r/min)，则轴所受的外力偶矩。

3、扭矩和扭矩图

    圆轴扭转时，截面上的内力矩称为扭矩，用T表示。扭矩的正负号，按右手螺旋法则判定。如扭矩矢量与截面外向法线一致，为正扭矩，反之为负；求扭矩时仍采用截面法。扭矩图是扭矩沿轴线变化图形，与轴力图的画法是相似

4、纯剪切   切应力互等定理

    单元体的左右两个侧面上只有切应力而无正应力，此种单元体发生的变形称为纯剪切。

在相互垂直的两个平面上，切应力必然成对存在且数值相等，两者都垂直于两个平面的交线、方向到共同指向或共同背离积这一交线，这就是切应力互等定理。

5、切应变  剪切虎克定律

   对于纯剪切的单元体，其变形是相对两侧面发生的微小错动，以γ来度量错动变形程度，即称切应变。

   当切应力不超过材料的剪切比例极限时，切应力τ和切应变γ成正比，即

τ=Gγ

G称材料的剪切弹性模量，常用单位是GPa。

6、圆杆扭转时的应力和强度计算

(1) 圆杆扭转时，横截面上的切应力垂直于半径，并沿半径线性分布，距圆心为ρ处的切应力为

式中T为横截面的扭矩，Ip为截面的极惯性矩。

(2) 圆形截面极惯性矩和抗扭截面系数

实心圆截面，     （D为直径）

空心圆截面，   

（D为外径，d为内径，）

(3)圆杆扭转时横截面上的最大切应力发生在外表面处

式中Wt=Ip/R，称为圆杆抗扭截面系数（或抗抟截面模量）。

圆杆扭转时的强度条件

(4)圆杆扭转时，圆杆各点处于“纯剪切”应力状态，如图3—1所示。其最大拉应力、最大压应力和最大切应力数值相等。

   低碳钢材料抗拉与抗压的屈服强度相等，抗剪能力较差，所以低碳钢材料圆杆扭转破坏是沿横截面被剪断的。

   铸铁材料抗压能力最强，抗剪能力次之，抗拉能力最差，因而铸铁材料圆杆扭转破坏是沿与杆轴线约成450的斜截面被拉断的。

7、圆杆扭转时的变形和刚度计算

   圆杆扭转时的变形用一个横截面相对另一个横截面转过的角度来度量，称为扭转角。

   长度为l的等截面圆杆承受扭矩Mn时，圆杆两端的相对扭转角

   （rad）

式中GIp称为圆杆的抗扭刚度。

   当两截面之间的扭矩或GIp为变量时则应通过积分或分段计算各段的扭转角，并求其代数和，即为全杆的扭转角。

单位长度扭转角             （rad/m）

把弧度换算为度，圆杆扭转时的刚度条件为

   （0/m）

8、非圆截面杆的扭转

(1)  非圆截面杆扭转的概念

非圆截面杆在扭转变形后横截面不再是平面，变成一个曲面并发生翘曲，这是非圆截面杆扭转时的一个重要特征。由于截面的翘曲，平面假设不再成立，因而圆杆的扭转公式不能应用于非圆截面杆。

(2) 矩形截面杆

   矩形截面杆扭转时，由切应力互等定理可知，横截面周边上的切应力和周边相切，角点处切应力为零。横截面上最大切应力发生在长边的中点处。

   设矩形截面杆长为l，承受扭矩T，矩形截面的长为h，宽为b。

最大切应力           

杆两端的相时扭转角

式中α，β是与长宽比h/b相关的系数，计算时可查阅有关手册。

     当长宽比时，称为狭长矩形，α，β可近似为1/3。

二、重点与难点

1、受扭杆件所受的外力偶矩，常由杆件所传递的功率及其转速来换算。

2、圆杆扭转时，横截面上切应力沿半径线性分布，并垂直于半径，最大切应力在外表面处。

3、低碳钢材料圆杆扭转破坏时，将沿横截面被剪断。铸铁材料圆杆扭转破坏时，将沿与杆轴线成450螺旋面被拉断。

三、解题方法要点

1、

2、

4.2典型题解

一、计算题

  等截面传动轴的转速n=150r/min，由A转输入功率NA=8kW，由B、C、D各轮输出功率分别为NB=3kW，NC=1kW，ND=4kW。己知轴的许用剪应力[τ]=60MPa，剪切弹性模量G=80GPa，[θ]=20/m。要求首先安排各轮的位置，然后绘出传动轴的扭矩图，并确定轴的直径。

   解：四轮各位置如图，其中A轮应放在轴的中间位置，使得从A轮输入的扭矩由该轮的两侧分担，不会使轴的某段承担输入的全部扭矩。根据功率转化为扭矩关系，A、B、C、D各点的扭矩

   己知各轮承担的扭矩后，由截面法可得各截面的扭矩，扭矩图如图。从扭矩图可知，最大扭矩应在DA、AB段，为

最大剪应力为

强度条件为

得到

              (1)

由于轴为等截面的，最大单位长度的扭转角也应在DA、AB段，等圆截面杆的单位长度的扭转角

刚度条件为

得

    (2)

从式(1)和式(2)中选择较大的作为轴的直径，可同时满足刚度和强度条件，轴的直径

d=31mm

二、计算题

一为实心、一为空心的两根圆轴，材料、长度和所受外力偶均一样，实心直径d1 ，空心轴外径D2 、内径d2 ，内外径之比α=d2/D2=0.8。若两轴重量一样，试求两轴最大相对扭转角之比。

解：两轴材料、重量和长度一样，则截面积也一样 A1=A2 ，即

可得

因承受的外力偶矩相同，两轴截面上扭矩也应相等 T1=T2 。

实心轴和空心轴最大相对扭转角分别是

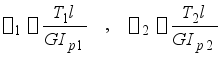
式中，l为轴的长度。故两轴最大相对扭转角之比

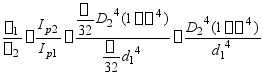
将代入上式，则

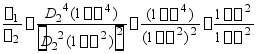
再将α＝0.8 代入上式，得

    可见，空心轴的扭转角远小于实心轴的。因此，采用空心圆轴不仅强度高，而且刚度也远优于实心圆轴。

三、计算题

    两个受扭薄壁杆截面，一个是开有纵向细缝的开口薄壁圆环，另一个是闭口薄壁圆环，如图所示。两杆的材料相同，尺寸相同，平均直径D=40mm，壁厚t=2mm，长度为l。两杆承受的扭矩相同。试求两杆最大切应力之比及扭转角之比。

解   (1) 开口薄壁圆环

开口薄壁圆环可以看成一个长为、宽为t的狭长矩形，则最大切应力

扭转角

(2) 闭口薄壁圆环

最大切应力

扭转角

对于薄壁圆环，Ip可以写成

因此

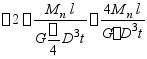
(3) 两杆最大切应力之比

两杆扭转角之比

   讨论：由本题的计算结果可以看出，闭口薄壁圆环的切应力及扭转角要比开口薄壁圆环小得多，因而在薄壁构件中应尽量采用闭口薄壁杆件。

4.3 练习题

一、概念题

1、问答题

低碳钢、铸铁及木材（顺纹方向与轴线平行）的圆棒两端受力偶作用，如图所示，直到破坏。试画出三种棒破坏时裂纹的方向，并说明为什么从此方向破坏。

2、是非判断题

（1）  圆杆受扭时，杆内各点处于纯剪切状态。（ 对 ）

（2） 杆件受扭时，横截面上的最大切应力发生在距截面形心最远处。（ 错 ）

（3）  薄壁圆管和空心圆管的扭转切应力公式完全一样。（ 错   ）

（4）  圆杆扭转变形实质上是剪切变形。（  对  ）

（5）  非圆截面杆不能应力用圆杆扭转切应力公式，是因为非圆截面杆扭转时“平截面假设”不能成立。（  对  ）

(6)  材料相同的圆杆，它们的剪切强度条件和扭转强度条件中，许用应力的意义相同，数值相等。（ 对 ）

(7)  剪断钢板时，所用外力使钢板产生的应力稍大于材料的屈服极限。（ 错 ）

(8)  矩形截面杆自由扭转时，横截面上的剪应力呈线性分布。（ 错 ）

3、选择题

（1） 阶梯圆轴的最大切应力发生在（ D ）。

A   扭矩最大的截面；               B    直径最小的截面

C   单位长度扭转角最大的截面       D    不能确定

（2） 空心圆轴的外径为D，内径为d，=d /D。其抗扭截面系数为（D ）。

A                  B  

C                 C  

（3） 扭转切应力公式适用于（ D ）杆件。

A   任意截面；                     B   任意实心截面；

C   任意材料的圆截面               D   线弹性材料的圆截面。

（4） 单位长度扭转角与（ A ）无关。

A   杆的长度；                     B   扭矩

C   材料性质；                     D   截面几何性质。

（5） 图示圆轴由钢杆和铝套管牢固地结合在一起。扭转变形时，横截面上切应力分布如图（  B   ）所示。

（6）若将受扭实心圆轴的直径增加一倍，则其刚度是原来的（ D ）。

A   2倍                           B   4倍

C   8倍                           D   16倍

(7) 空心圆轴，其内外径之比为，扭转时轴内的最大剪应力为，这时横截面上内边缘的剪应力为（ B ）。

　             Ａ   　　　　                    Ｂ    　　　　

Ｃ　 零　　　　　                  Ｄ　

(8) 实心圆轴扭转，己知不发生屈服的极限扭矩为T0，若将其横截面积增加１倍，那么极限扭矩是（　C　）。

Ａ  　　                       Ｂ   　　　

Ｃ  　　　                    Ｄ  

(9)  对于受扭的圆轴，关于如下结论：

     ① 最大剪应力只出现在横截面上；

     ② 在横截面上和包含杆件的纵向截面上均无正应力；

     ③ 圆轴内最大拉应力的值和最大剪应力的值相等。

现有四种答案，正确的是（   A   ）。

A  ②③对                           B  ①③对      

         C  ①②对                           D  全对

二、计算题

1、 试用截面法求出图示圆轴各段内的扭矩T，并作扭矩图。

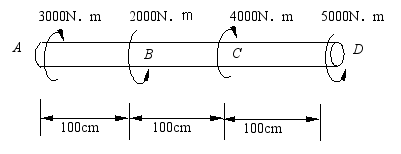
答：

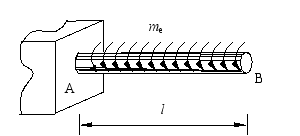
2、 图示一齿轮传动轴，传递力偶矩Me=10kN．m,轴的直径d=80mm.。试求轴的最大切应力。

答：τmax=100MPa

3、 设将例题4—2中直径d=0.０６m的实心圆轴制成外径Ｄ与内径d之比为３／２的空心圆轴，仍受力偶矩Ｍe＝２.５kN．m的作用。试求：使τmax与该例题相同时，能节省多少材料？

答：D＝0.065m

4、 图示一圆锥形杆AB，受力偶矩Me作用，杆长为l，两端截面的直径分别为d1和d2=1.2d1，材料的切变模量为G。试求：（1）截面A和B的扭转角，（2）若按平均直径的等直杆计算扭转角，误差等于多少？

答：

5、 如图所示的空心圆轴，外径D=100mm，内径d=80mm， l=500mm，M1=6kNm，M2=4kNm,材料的剪切弹性模量G=80GPa。请绘轴的扭矩图，并求出最大剪应力。

答：

6、 在图题3.9所示两端嵌固的圆轴上，外扭矩Me1=2Me2，距离a=c=L/4，b=L/2，圆轴直径为d，试求此圆轴横截面上的最大切应力。

答：                        

7、  图示传动轴，主动轮B输入功率P1=368kW,从动轮A，阵C输出的功率分别为P2=147kW, P3=221kW, 轴的转速n=500r/min,材料的G=80GPa，许用切应力=70MPa，许用单位长度扭转角=10/m。（1）画出轴的扭矩图；（2）设计轴的直径；（3）讨论提高轴强度和刚度的措施

答：d=85mm

8、 钻探机钻杆的外径D=60mm，内径d=50mm，切率P=7.355kW,轴的转速n=180r/min，钻杆钻入土层的深度l=40m，材料的切变模量G=80GPa，许用切应力=40MPa，假设土壤对钻杆的阻力沿长度均匀分布，试求：（1）土壤对钻杆单位长度的阻力矩m；（2）作钻杆的扭矩图，并进行强度校核；（3）计算A、B截面的相对扭转角。

答：

9、 用实验方法求钢的切变模量G时，其装置的示意图如图所示。AB为直径d=10mm，长度l=0.1m的圆截面钢试件，A端固定，B端有长s=80mm的杆BC与截面联成整体。当在B端加转矩T=15N.m时，测得BC杆顶点C有位移=1.5mm。试求：（1）切变模量；（2）杆内的最大切应力；（3）杆表面的切应变。

答：

10、 图示一传动轴，主动轮I传递力偶矩1kN．m，从动轮Ⅱ传递力偶0.4kN．m，从动轮Ⅲ传递力偶矩0.6kN．m.。己知轴的直径d=40mm，各轮间距l=500mm，材料的切变模量G=80GPa。要求（1）合理布置各轮的位置；（2）求出轴在合理位置时的最大切应力和最大扭转角。

答：=47.8MPa,   =0.015rad

11、 图示某带轮传动轴，己知：P=14kW，n=300r/min，=40MPa，=0.01rad/min，G=80GPa。试根据强度和刚度条件计算两种截面的直径：（1）实心圆截面的直径d；（2）空心圆截面的内径d1和外径d2（d1/ d2=3/4）

答：d≥49mm， d2≥53.7 mm

12、 图示一圆截面杆，左端固定，右端自由，在全长范围内受均布力偶矩作用，其集度为me。设杆的材料的切变模量为G，截面的极惯性矩为Ip，杆长为l。试求自由端的扭转角。

答：=

13、 一薄壁钢管受扭矩Me=2kN．m作用。己知D=60mm，d=50mm，E=210GPa。己测得管表面上相距l=200mm的AB两截面的相对扭转角=0.430，试求材料的泊松比。

答：μ=0.3

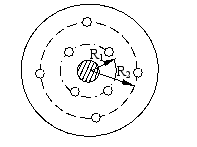
14、 一联轴器，由分别分布在半径为R1和R2圆周上的8只直径相同的螺栓相联接  （如图所示）。则内圈（R1）螺栓横截面上的切应力与外圈（R2）螺栓截面上的切应力的比值为（     ）。

   A）；  （B）；  （C）；  （D）

15、 试作图4—32所示各轴的扭矩图，并求出及其作用处。

16、  齿轮轴上有四个齿轮,见图4­—33,己算出各轮所受外力偶矩为mA=52N•m、mB=120N·m、mC=40N·m、mD=28N·m.己知各段轴的直径分别为dAB=15mm、dBC=20mm、dCD=12mm。

  ①作该轴的扭矩图；

②求职1-2、 2-3、 3-3截面上的最大切应力。

17、  图4—37所示圆轴的AC段为实心圆珠笔截面,CB段为实心圆截面,外径D=30mm,空心段内径d=20mm、外力偶矩m=200N·m,试计算AC段和CB段横截面外边缘的切应力,以及CB段内边缘处的切应力。

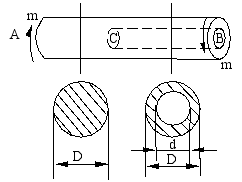
18、  图4—38所示实心圆轴通过牙嵌离合器把功率传给空心圆轴。传递的功率N=7.5kW,轴的转速n=80r/min。试选择实心圆轴的直径d和空心圆轴的外径d2。己知空心圆轴的内外径之比1=d1/d2=0.8,许用扭转切应力=40MPa。

19、   阶梯形圆轴直径分别为d1=40mm,d2=70mm,轴上装有三个皮带轮,如图所示。己知由轮3输入的功率为N3=3kW,轮1输出的功率为N1=13kW,轴作匀速转动,转速n=200r/min,材料的许用切应力=60MPa,G=80GPa,许用扭转角=20/m。试校核轴的强度和刚度。

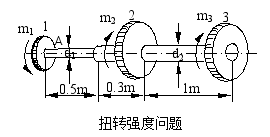
20、 传动轴的转速为n=500r/min，如图所示，主动轮1输入功率N1=368kN.m/s，从动轮2、3分别输出功率N2=147kN·m/s,N3=221kN·m/s。己知=70MPa，=10/m，G=80GPa。

①试确定AB段的直径d1和BC段的直径d2。

② 若AB和BC两段选用同一直径,试确定直径d.。

③主动轮和从动轮应如何安排才比较合理?

21、  悬臂圆轴AB,承受均布外力偶矩t的作用,试导出该杆B端扭转角的计算公式(见图示)

22、  阶梯形实圆轴承受扭转变形，圆轴最大剪应力=_________。

23、  如图所示的空心圆轴，外径D=100mm，内径d=80mm，l=500mm，M1=6kNm，M2=4kNm，材料的剪切弹性模量G=80GPa。请绘轴的扭矩图，并求出最大剪应力。

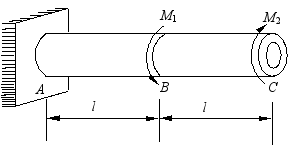
24、 图示等截面传动轴的转速为500r/min，主动轮A输入功率368kW，从动轮B和C分别输出功率147kW和221kW。己知许用剪应力=70MPa，许用单位长度扭转角=10/m，材料的剪切弹性模量G=80GPa。试：

（1）设计传动轴的直径d；

（2）举出一个提高传动轴承载能力的方法，并简述其理由。

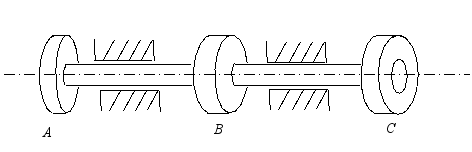
25、 两端固定的实心圆杆，其AC段的直径为2d,CB段的直径为d，试求在图示扭矩TC作用下，固定端A、B处的反扭矩以及C截面的扭转角。

26、  试作图示圆轴的扭矩图，并求B截面相对A截面的相对扭角及AB段中最大相对扭转角（相对于截面A）。设T，α,G，d均为已知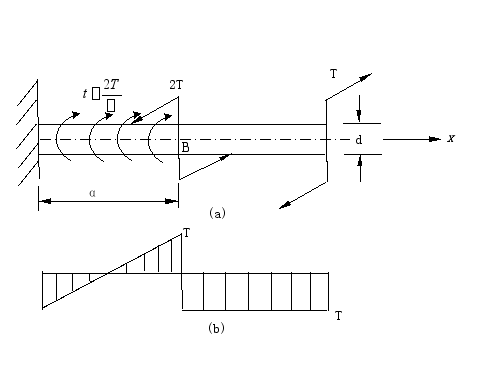，t是均布扭转力偶矩的集度