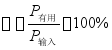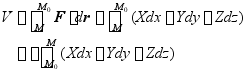§14-1质系动能定理
§14-1质系动能定理
1.质点动能定理
牛顿第二定律给出

上式两边点乘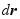 ,得
,得

因  ,于是上式可写为
,于是上式可写为

或  (14-1)
(14-1)
式中 称为质点的动能,
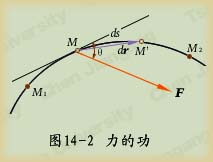
称为质点的动能, 称为力的元功。参看图14-1。式(14-1)称为质点动能定理的微分形式,即作用于质点上力的元功等于质点动能的微分。
称为力的元功。参看图14-1。式(14-1)称为质点动能定理的微分形式,即作用于质点上力的元功等于质点动能的微分。
将上式积分,得

 (14-2)
(14-2)
式中  为作用于质点上的力在有限路程上的功。式(14-2)为质点动能定理的积分形式,即作用于质点上的力在有限路程上的功等于质点动能的改变量。
为作用于质点上的力在有限路程上的功。式(14-2)为质点动能定理的积分形式,即作用于质点上的力在有限路程上的功等于质点动能的改变量。
2.质系动能定理
设质系由 个质点组成,其中任意一质点,质量为
个质点组成,其中任意一质点,质量为 ,速度为
,速度为 ,作用于该质点上的力为
,作用于该质点上的力为 。根据质点动能定理的微分形式有
。根据质点动能定理的微分形式有
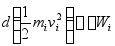

 个方程相加,得
个方程相加,得 
交换微分及求和的次序,有 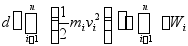
式中 为质系内各质点动能的和,称为质系的动能,常用
为质系内各质点动能的和,称为质系的动能,常用 表示,所以质系动能
表示,所以质系动能
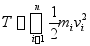 (14-3)
(14-3)
 为作用于质系上所有力的元功之和。所以得出质系动能定理的微分形式:在质系无限小的位移中,质系动能的微分等于作用于质系全部力所做的元功之和。即
为作用于质系上所有力的元功之和。所以得出质系动能定理的微分形式:在质系无限小的位移中,质系动能的微分等于作用于质系全部力所做的元功之和。即
 (14-4)
(14-4)
对上式积分,得
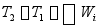 (14-5)
(14-5)
 和
和 分别表示质系在任意有限路程的运动中起点和终点的动能。式(14-5)为质系动能定理的积分形式:质系在任意有限路程的运动中,起点和终点动能的改变量,等于作用于质系的全部力在这段路程中所做功的和。
分别表示质系在任意有限路程的运动中起点和终点的动能。式(14-5)为质系动能定理的积分形式:质系在任意有限路程的运动中,起点和终点动能的改变量,等于作用于质系的全部力在这段路程中所做功的和。
§14-3质系和刚体的动能
1. 质系的动能
设质系由 个质点组成,任一质点
个质点组成,任一质点 在某瞬时的动能为
在某瞬时的动能为 ,质系内所有质点在某瞬时动能的算术和称为该瞬时质系的动能,以
,质系内所有质点在某瞬时动能的算术和称为该瞬时质系的动能,以 表示,即
表示,即
` (14-18)
(14-18)
动能是描述质系运动强度的一个物理量。动能的单位与功的单位相同。
2.平动刚体的动能
当刚体平动时,刚体上各点速度相同,于是平动刚体的动能为
 (14-19)
(14-19)
3.定轴转动刚体的动能
当刚体绕固定轴 转动时,如下页图14-9所示,其上任一点的速度为
转动时,如下页图14-9所示,其上任一点的速度为

于是绕定轴转动刚体的动能为

 为刚体对
为刚体对 轴的转动惯量,所以得
轴的转动惯量,所以得

 (14-20)
(14-20)
 4.平面运动刚体的动能
4.平面运动刚体的动能
刚体作平面运动时,可视为绕通过速度瞬心 并与运动平面垂直的轴的转动,动能可写为
并与运动平面垂直的轴的转动,动能可写为

根据转动惯量的平行轴定理有
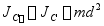
代入上式得
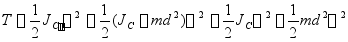
而 是质心
是质心 的速度的大小,因此
的速度的大小,因此
 (14-21)
(14-21)
式(14-20)表明,平面运动刚体的动能等于跟随质心平动的动能与绕通过质心的转轴转动的动能之和。
§14-4动能定理应用举例
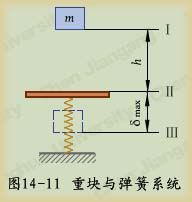 例14-1质量为
例14-1质量为 的物块,自高度
的物块,自高度 处自由落下,落到有弹簧支承的板上,如图14-11所示。弹簧的刚性系数为
处自由落下,落到有弹簧支承的板上,如图14-11所示。弹簧的刚性系数为 ,不计弹簧和板的质量。求弹簧的最大变形。
,不计弹簧和板的质量。求弹簧的最大变形。
解:分为两个阶段
1.重物由位置Ⅰ落到板上。在这一过程中,只有重力做功,应用动能定理,有
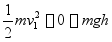
求得
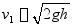
2.物块继续向下运动,弹簧被压缩,物块速度逐渐减小,当速度等于零时,弹簧被压缩到最大变形 。在这一过程中,重力和弹性力均做功。应用动能定理,有
。在这一过程中,重力和弹性力均做功。应用动能定理,有

解得
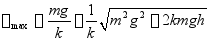
由于弹簧的变形量是正值,因此取正号,即

·上述两个阶段,也可以合在一起考虑,即
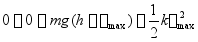
解得的结果与前面所得相同。
·上式说明,在物块从位置Ⅰ到位置Ⅲ的运动过程中,重力做正功,弹性力做负功,恰好抵消,因此物块运动始末位置的动能是相同的。显然,物块在运动过程中动能是变化的,但在应用动能定理时不必考虑始末位置之间动能是如何变化的。
 例14-2提升机构如图14-12所示,设启动时电动机的转矩
例14-2提升机构如图14-12所示,设启动时电动机的转矩 视为常量,大齿轮及卷筒对于轴
视为常量,大齿轮及卷筒对于轴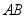 的转动惯量为
的转动惯量为 ,小齿轮、联轴节及电动机转子对于轴
,小齿轮、联轴节及电动机转子对于轴 的转动惯量为
的转动惯量为 ,被提升的重物重为
,被提升的重物重为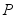 ,卷筒、大齿轮及小齿轮的半径分别为
,卷筒、大齿轮及小齿轮的半径分别为 及
及 。略去摩擦及钢丝绳质量,求重物从静止开始上升距离
。略去摩擦及钢丝绳质量,求重物从静止开始上升距离 时的速度及加速度。
时的速度及加速度。
解:1、以整个系统(包括电机)为研究对象;
2、计算主动力的功:系统所受的约束为理想约束,只有电动机的转矩 和重力
和重力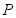 做功,则
做功,则 
3、计算系统始末位置的动能:系统由静止状态开始运动,所以初始位置的动能
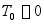
当重物上升高度 时,此时重物的速度
时,此时重物的速度 ,轴
,轴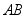 和
和 的角速度分别为
的角速度分别为 和
和 ,系统在此位置的动能为
,系统在此位置的动能为

4、应用动能定理,并求解重物的速度:
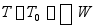
列出方程

运动学关系 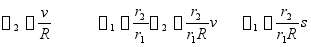
得
 ①
①
所以,重物的速度
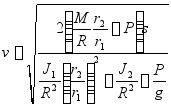
·上式建立了重物的速度与上升距离之间的关系。在一般情况下,对于一个自由度系统应用动能定理可直接建立系统的速度与系统的位移之间的关系。
5、求重物的加速度
将式①两边对时间求导数,并注意到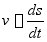 及
及 的关系,可得,
的关系,可得,


由此得

·由上面加速度 的表达式中可看出,分母恒为正值。在启动时
的表达式中可看出,分母恒为正值。在启动时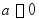 ,故要求驱动力矩
,故要求驱动力矩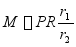 ,启动后若重物匀速上升,
,启动后若重物匀速上升, ,此时
,此时 。
。
例14-3卷扬机如图14-13所示。鼓轮在常力偶矩 作用下将圆柱体沿斜面上拉。已知鼓轮的半径为
作用下将圆柱体沿斜面上拉。已知鼓轮的半径为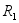 ,质量为
,质量为 ,质量分布在轮缘上;圆柱体的半径为
,质量分布在轮缘上;圆柱体的半径为 ,质量为
,质量为 ,质量均匀分布。设斜面的倾角为
,质量均匀分布。设斜面的倾角为 ,圆柱体沿斜面只滚不滑。系统从静止开始运动,求圆柱体中心
,圆柱体沿斜面只滚不滑。系统从静止开始运动,求圆柱体中心 的速度与其路程之间的关系。
的速度与其路程之间的关系。
解:1、以鼓轮和圆柱体组成的整个系统作为分析对象;
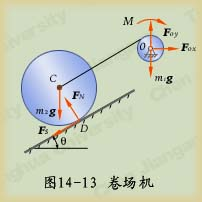 2、分析系统的受力并计算力的功:主动力有重力
2、分析系统的受力并计算力的功:主动力有重力 和
和 以及主动力偶矩
以及主动力偶矩 ;约束力有
;约束力有 及
及 ,如图14-13所示。因为
,如图14-13所示。因为 点的位移为零,所以
点的位移为零,所以 的功为零,而圆柱体沿斜面只滚不滑,轮缘上与斜面的接触点为瞬心,法向约束力
的功为零,而圆柱体沿斜面只滚不滑,轮缘上与斜面的接触点为瞬心,法向约束力 与静滑动摩擦力
与静滑动摩擦力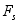 也不做功。因此所分析的系统为具有理想约束的一个自由度系统。主动力的功为
也不做功。因此所分析的系统为具有理想约束的一个自由度系统。主动力的功为

3、分析系统的运动并计算动能:
系统的动能
式中 分别为鼓轮对于中心轴
分别为鼓轮对于中心轴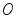 ,圆柱体对于过质心
,圆柱体对于过质心 的轴的转动惯量,有
的轴的转动惯量,有

 分别为鼓轮和圆柱体的角速度,有如下关系
分别为鼓轮和圆柱体的角速度,有如下关系
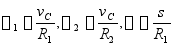
代入后得

4、应用质系动能定理并求解:质系动能定理

有
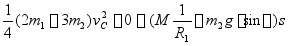
所以的,得

·读者还可以继续求圆柱体中心 的加速度。
的加速度。
小结
1.具有理想约束的一个自由度系统,应用动能定理可直接建立系统的速度量与位移量之间的关系;进一步对时间求导数,可求出系统的加速度量。所以,在这种情形下应用动能定理求解已知力求运动的问题是很方便的。
2.应用动能定理解题的步骤:
(1)明确分析对象,一般以整个系统为研究对象;
(2)分析系统的受力,区分主动力与约束力,在理想约束的情况下约束力不做功;
(3)分析系统的运动,计算系统在任意位置的动能或在起始和终了位置的动能;
(4)应用动能定理建立系统的动力学方程,而后求解;
(5)对问题的进一步分析与讨论。
§14-5功率、功率方程、机械效率
1功率
单位时间内力所做的功。用功率来衡量机器做功的快慢程度,是衡量机器性能的一项重要指标。
力 的元功为
的元功为 
则力的功率为
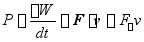 (14-22)
(14-22)
上式表明:力的功率等于力在力的作用点的速度方向上的投影与速度的乘积。
力矩或转矩 的元功为
的元功为
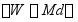
则力矩或转矩的功率为
 (14-23)
(14-23)
上式表明:力矩或转矩的功率等于力矩与物体转动的角速度的乘积。
功率的单位是焦耳/秒 ,称为瓦
,称为瓦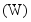

若转动角速度用转速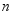 (单位为
(单位为 )给出,转矩的单位为
)给出,转矩的单位为 ,则式(14-23)可改写为工程中常用的形式
,则式(14-23)可改写为工程中常用的形式
 (14-24)
(14-24)
或写为转矩的表达式
 (14-25)
(14-25)
2.功率方程
任何机器工作时必须输入一定的功,用 表示,机器做了有用功,用
表示,机器做了有用功,用 表示,同时机器要克服无用阻力,消耗一部分功,用
表示,同时机器要克服无用阻力,消耗一部分功,用 表示。根据动能定理的微分形式,有
表示。根据动能定理的微分形式,有

将上式两边除以对应的时间间隔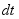 ,并以
,并以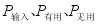 分别表示发动机输入的功率,有用阻力消耗的功率和无用阻力消耗的功率,则
分别表示发动机输入的功率,有用阻力消耗的功率和无用阻力消耗的功率,则
 (14-26)
(14-26)
上式称为机器的功率方程,它表示任一机器输入、输出功率和机器动能变化率之间的关系。
当机器启动或加速运动时, ,故要求
,故要求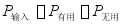 ,即输入功率要大于输出功率;
,即输入功率要大于输出功率;
当机器停车或负荷突然增加时,机器做减速运动, ,此时
,此时 ,即输入功率小于输出功率;
,即输入功率小于输出功率;
当机器匀速运转时, ,
, ,即输入功率和输出功率相等,称为功率平衡。
,即输入功率和输出功率相等,称为功率平衡。
3.机械效率
机械在稳定运转时,有用输出功率与输入功率之比。用 表示,即
表示,即
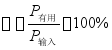 (14-27)
(14-27)
机械效率说明机械对于输入能量的有效利用程度,是评价机械质量的指标之一。它与机械的传动方式、制造精度与工作条件有关,一般情况下 。
。
 例14-4车床电动机的功率
例14-4车床电动机的功率 ,当稳定运转时主轴的转速为
,当稳定运转时主轴的转速为 ,如图14-14所示,设转动时由于摩擦而损耗的功率是输入功率的30%,工件的直径
,如图14-14所示,设转动时由于摩擦而损耗的功率是输入功率的30%,工件的直径 ,求此转速下的切削力。
,求此转速下的切削力。
解:车床稳定运转时, ,输入功率与输出功率相等。即
,输入功率与输出功率相等。即

而 ,代入上式得
,代入上式得

 表示切削力的功率,如图14-14所示,即
表示切削力的功率,如图14-14所示,即

得

例14-5胶带运输机如图14-15所示,已知胶带的速度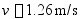 ,运输量
,运输量 ,提升高度
,提升高度 ,机械效率
,机械效率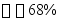 。求运输机所需的电动机功率。
。求运输机所需的电动机功率。
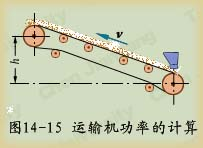
解:取整段胶带上被运输的物料为研究对象。
在 时间间隔内有质量为
时间间隔内有质量为 的物料被提升到高度
的物料被提升到高度 处,则重力所作的功为
处,则重力所作的功为
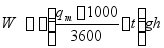
在 时间间隔内有有同样多的物料又补充到胶带上,而且它们的速度由零变为
时间间隔内有有同样多的物料又补充到胶带上,而且它们的速度由零变为 ,因此系统动能的变化为
,因此系统动能的变化为

设电动机的功率为 ,由于机械效率
,由于机械效率 ,所以在
,所以在 秒内所做的有用功为
秒内所做的有用功为

由动能定理

得 
消去 后得
后得

=
可根据算出的功率选择所需的电动机。
§14-6势力场、势能、机械能守恒定律
1势力场:
如质点在某空间内任一位置都受有一个大小和方向完全由所在位置确定的力作用,具有这种特性的空间就称为力场,例如地球表面的空间为重力场。如质点在某一力场内运动时,力场力对于质点所做的功仅与质点起点与终点位置有关,而与质点运动的路径无关,则这种力场称为势力场或保守力场。质点在势力场内所受的力称为势力或保守力。如重力、弹性力及万有引力都是势力。
2.势能、势能函数
势能:在势力场中质点从某一位置 移至选定的基点
移至选定的基点 的过程中势力所做的功。以
的过程中势力所做的功。以 表示,即
表示,即
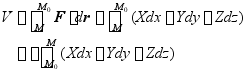 (14-28)
(14-28)
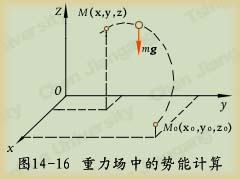
(1)重力场中的势能:如图14-16所示重力的势能为

为了计算方便,取基点的位置 ,上式可写为
,上式可写为

对于质点系或刚体
 (14-29)
(14-29)
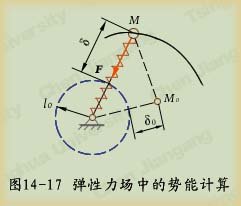
 其中
其中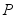 是系统的重量,
是系统的重量,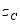 是质心的坐标。
是质心的坐标。
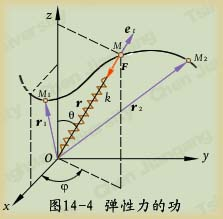
(2)弹性力场中的势能:在弹性力场中

式中 和
和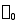 分别为弹簧端点在
分别为弹簧端点在 和
和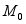 时弹簧的变形量。如取弹簧的自然位置为基点,有
时弹簧的变形量。如取弹簧的自然位置为基点,有 ,于是得
,于是得
 (14-30)
(14-30)
(3)万有引力场中的势能:如图14-18所示, 为质量为
为质量为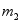 的物体作用于质量为
的物体作用于质量为 的物体上的万有引力,取
的物体上的万有引力,取 点为势能基点,则万有引力在
点为势能基点,则万有引力在 点的势能为
点的势能为


得

如势能基点选在无穷远处,即 ,得
,得
 (14-31)
(14-31)
势能函数:由上面的讨论可以看出,质点或质系的势能仅与质点或质心的位置有关,在一般情形下,质点或质系的势能只是质点或质心坐标的单值连续函数,这个函数称为势能函数,可表示为

势能函数相等的各点所组成的曲面称为等势面,表示为


 如重力场的等势面是不同高度的水平面,如图14-19(a)。弹性力场的等势面是以弹簧固定端为中心的球面,如图14-19(b)。地球引力场的等势面是以地心为中心的不同半径的同心球面。
如重力场的等势面是不同高度的水平面,如图14-19(a)。弹性力场的等势面是以弹簧固定端为中心的球面,如图14-19(b)。地球引力场的等势面是以地心为中心的不同半径的同心球面。
当 时的等势面称为零等势面,若选零等势面为势能的基面(零势面),某一位置的势能等于势能函数在该位置的函数值。例如在重力场中,一般选水平面为零势面;在弹性力场中选弹簧自由长度,初变形为零处为零势能位置;万有引力场中选无穷远处为零势能位置。
时的等势面称为零等势面,若选零等势面为势能的基面(零势面),某一位置的势能等于势能函数在该位置的函数值。例如在重力场中,一般选水平面为零势面;在弹性力场中选弹簧自由长度,初变形为零处为零势能位置;万有引力场中选无穷远处为零势能位置。
 3.机械能守恒定律
3.机械能守恒定律
保守系统:具有理想约束,且所受的主动力皆为势力的质系称为保守系统。
对于保守系统,动能定理

式中 应为系统中所有势力的功之和。
应为系统中所有势力的功之和。
势力的功与路径无关,可通过势能计算 。如图14-20所示,设质点在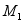 和
和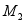 处的势能分别为
处的势能分别为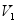 和
和 。如以
。如以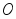 点为零势点,则
点为零势点,则

因势力的功与路径无关

上述结论可直接推广到质系:即质系从位置Ⅰ运动到位置Ⅱ时,势力的功等于质系在位置Ⅰ时的势能和在位置Ⅱ时的势能之差。由此得
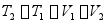
式中 和
和 分别为质系在位置Ⅰ时的势能和在位置Ⅱ时的势能。所以
分别为质系在位置Ⅰ时的势能和在位置Ⅱ时的势能。所以

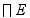 (常量) (14-32)
(常量) (14-32)
 ,即质系在某瞬时的动能与势能的代数和称为机械能。
,即质系在某瞬时的动能与势能的代数和称为机械能。
式(14-32)称为质系机械能守恒定律,即保守系统在运动过程中,其机械能保持不变。或质系的动能和势能可以互相转化,但总的机械能保持不变。
因为势力场具有机械能守恒的特性,因此势力场又称为保守力场,而势力又称为保守力。质系在非保守力作用下运动时,则机械能不守恒。例如摩擦力做功时总是使机械能减少,但是减少的能量并未消失,而是转化为另一形式的能量(热能),总能量仍然是守恒的。如果考虑了各种形式的能量(如电磁能、化学能、热能等)的转化时,对于整个系统来说,总的能量仍是守恒的,这就是普遍形式的能量守恒定律,机械能守恒定律只不过是它的特殊情形。
 例14-6试用机械能守恒定律解例14-1题。
例14-6试用机械能守恒定律解例14-1题。
解:选图14-11中位置Ⅰ作为运动的初始位置,位置Ⅲ作为运动的终了位置,则系统的动能

势能的零位可任意选,这里不妨取弹簧未变形时的位置作为弹性力势能的零位,取终了位置Ⅲ作为重力势能的零位。于是初始位置与终了位置的势能分别为

根据机械能守恒定律

将上述各值代入后得

与例14-1中所得结果完全相同。读者可选择不同的势能零位进行分析计算。
例14-7计算第二宇宙速度。
解:第二宇宙速度是物体能脱离地球引力作星际航行的逃逸速度。地球引力的大小为

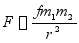
式中 分别为物体和地球的质量,
分别为物体和地球的质量, 为物体到地心的距离。当物体在地球表面时有
为物体到地心的距离。当物体在地球表面时有

故

式中 为地球的半径。物体在地球引力场内运动时,它的机械能是守恒的,设离地心无穷远处为势能零点,如图14-21所示在地球表面附近物体的速度为
为地球的半径。物体在地球引力场内运动时,它的机械能是守恒的,设离地心无穷远处为势能零点,如图14-21所示在地球表面附近物体的速度为 ,根据机械能守恒定律有
,根据机械能守恒定律有

 欲使物体脱离地球引力而永不返回,应使物体在无穷远处其动能为零,即
欲使物体脱离地球引力而永不返回,应使物体在无穷远处其动能为零,即 时
时 ,并考虑到
,并考虑到 ,有
,有
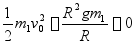
得

取地球半径 ,代入上式可解得
,代入上式可解得

此即为第二宇宙速度。
§14-7普遍定理的综合应用
质系动力学普遍定理包括质系动量定理、质系动量矩定理、质系动能定理。它们以不同的形式建立了质系的运动与受力之间的关系。动量定理和动量矩定理分别建立了质系动量和动量矩与质系所受外力系的主矢量和外力系的主矩之间的关系,它们是矢量形式的。动能定理建立了质系的动能与作用于质系上的力的功之间的关系,是标量形式的。
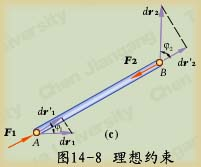
作用在系统上的力在动量和动量矩定理中一般按外力和内力分类。在动能定理中力一般按主动力和约束力分类,在理想约束的情形下约束力的功之和为零。
应用质系普遍定理可以解决质系动力学的两类问题。在实际应用中,对于具有理想约束的一个自由度系统,经常用动能定理解决已知力求运动的问题。在主动力为势力的情形下还可以应用机械能守恒定律求系统的运动。系统的运动规律确定后,一般用动量或动量矩定理求未知约束力。
例14-8质量为 ,半径为
,半径为 的均质圆柱体,在半径为
的均质圆柱体,在半径为 的固定大圆槽内作无滑动的滚动。试列写系统的运动微分方程。
的固定大圆槽内作无滑动的滚动。试列写系统的运动微分方程。
解:1、 以圆柱体为分析对象;
2、圆柱体的受力图如图14-22所示,在只滚不滑的情形下,摩擦力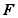 及正压力
及正压力 不做功,只有主动力
不做功,只有主动力 做功,所以为理想约束的情形;
做功,所以为理想约束的情形;
3、选 为广义坐标,正方向如图所示。系统的动能
为广义坐标,正方向如图所示。系统的动能
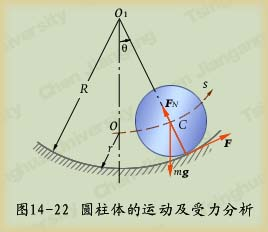

而
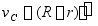


代入上式后得

4、应用动能定理建立系统的运动与受力之间的关系;
动能定理的微分形式给出

在理想约束的情形下, 为主动力的元功之和。图中
为主动力的元功之和。图中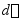 为广义坐标
为广义坐标 的微小增量,正方向如图所示。圆柱体质心
的微小增量,正方向如图所示。圆柱体质心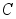 的微小位移为
的微小位移为 ,重力的元功为
,重力的元功为 。代入上式得
。代入上式得


两边同除以 ,得
,得

由此得到系统的运动微分方程为
 ①
①
5、讨论:
(1)本题也可用机械能守恒定律求解,设圆柱体的初始位置在质心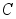 位于最低位置处,此时圆柱体的动能为
位于最低位置处,此时圆柱体的动能为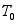 ,即给圆柱体一初始速度,势能
,即给圆柱体一初始速度,势能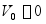 。圆柱体在任意位置的动能为
。圆柱体在任意位置的动能为

势能为

由机械能守恒定律

得

上式两边对时间求导数后,得到与式①完全相同的结果。
(2)由本题的分析可以看出,对于具有理想约束的一个自由度系统,可直接应用动能定理建立系统的运动与受力之间的关系,以解决已知力求运动的问题。
例14-9一矿井提升设备如图14-23所示。质量为 、回转半径为
、回转半径为 的鼓轮装在固定轴
的鼓轮装在固定轴 上,鼓轮上半径为
上,鼓轮上半径为 的轮上用钢索吊有一平衡重量
的轮上用钢索吊有一平衡重量 。鼓轮上半径为
。鼓轮上半径为 的轮上用钢索牵引矿车,车重
的轮上用钢索牵引矿车,车重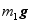 。设车在倾角为
。设车在倾角为 的轨道上运动。如在鼓轮上作用一常力矩
的轨道上运动。如在鼓轮上作用一常力矩 。求: (1)启动时矿车的加速度;
。求: (1)启动时矿车的加速度;
(2)两段钢索中的拉力;
(3)鼓轮的轴承约束力。不计各处的摩擦及车轮的滚动摩阻。

解:1、以整个系统作为分析对象,该系统为具有理想约束的一个自由度系统。首先应用质系动能定理,解决已知主动力求运动的问题。建立质系的动能方程,设初始时质系处于静止,鼓轮顺时针转过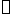 角后,有
角后,有

根据约束条件有以下运动学关系


代入上式后有

上式两边对时间求导数,并消去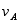 ,得矿车的加速度为
,得矿车的加速度为

2、求钢索拉力和鼓轮轴承约束力是已知运动求力的问题。分别以平衡重和鼓轮为分析对象,将钢索内力和约束力暴露出来,其受力图如图14-23(b)、(c)所示。应用动量定理有
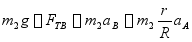
得

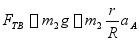
根据质系动量定理和动量矩定理列写鼓轮的动力学方程
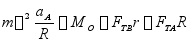

由以上三方程可分别求出 ,读者可自行完成。读者还可以取不同的分析对象,求钢索的拉力和轴承
,读者可自行完成。读者还可以取不同的分析对象,求钢索的拉力和轴承 的约束力。
的约束力。
 §14-1质系动能定理
§14-1质系动能定理![]()
![]() ,得
,得![]()
![]() ,于是上式可写为
,于是上式可写为![]()
![]() (14-1)
(14-1)![]() 称为质点的动能,
称为质点的动能,![]() 称为力的元功。参看图14-1。式(14-1)称为质点动能定理的微分形式,即作用于质点上力的元功等于质点动能的微分。
称为力的元功。参看图14-1。式(14-1)称为质点动能定理的微分形式,即作用于质点上力的元功等于质点动能的微分。![]()
![]() (14-2)
(14-2)![]() 为作用于质点上的力在有限路程上的功。式(14-2)为质点动能定理的积分形式,即作用于质点上的力在有限路程上的功等于质点动能的改变量。
为作用于质点上的力在有限路程上的功。式(14-2)为质点动能定理的积分形式,即作用于质点上的力在有限路程上的功等于质点动能的改变量。![]() 个质点组成,其中任意一质点,质量为
个质点组成,其中任意一质点,质量为![]() ,速度为
,速度为![]() ,作用于该质点上的力为
,作用于该质点上的力为![]() 。根据质点动能定理的微分形式有
。根据质点动能定理的微分形式有![]()
![]()
![]() 个方程相加,得
个方程相加,得 ![]()
![]()
![]() 为质系内各质点动能的和,称为质系的动能,常用
为质系内各质点动能的和,称为质系的动能,常用![]() 表示,所以质系动能
表示,所以质系动能![]() (14-3)
(14-3)![]() 为作用于质系上所有力的元功之和。所以得出质系动能定理的微分形式:在质系无限小的位移中,质系动能的微分等于作用于质系全部力所做的元功之和。即
为作用于质系上所有力的元功之和。所以得出质系动能定理的微分形式:在质系无限小的位移中,质系动能的微分等于作用于质系全部力所做的元功之和。即![]() (14-4)
(14-4)![]() (14-5)
(14-5)![]() 和
和![]() 分别表示质系在任意有限路程的运动中起点和终点的动能。式(14-5)为质系动能定理的积分形式:质系在任意有限路程的运动中,起点和终点动能的改变量,等于作用于质系的全部力在这段路程中所做功的和。
分别表示质系在任意有限路程的运动中起点和终点的动能。式(14-5)为质系动能定理的积分形式:质系在任意有限路程的运动中,起点和终点动能的改变量,等于作用于质系的全部力在这段路程中所做功的和。