引言
1.运动的相对性
在§6-6中,曾提到运动相对性的概念,在前两章中,总是把坐标系固结于地面来研究点和刚体的运动。此时认为地球固定不动。
 如果建立一地心坐标系来观察地球的运动,则地球绕地轴作自转,此时固结于地球上的坐标系随地球一起作定轴转动。
如果建立一地心坐标系来观察地球的运动,则地球绕地轴作自转,此时固结于地球上的坐标系随地球一起作定轴转动。
如果建立一日心坐标系;来观察地球的运动,则地球在自转的同时,还有绕太阳沿椭圆轨道的运动。
2.本章研究的范畴
本章引入相对于定系运动着的坐标系,称为动系,并研究一个点相对于这两个坐标系的运动以及它们之间的联系。
如图8-1所示一简单陀螺,框架AB绕Z作定轴转动,转子O相对于框架绕CD轴转动,同时随框架一起运动。转子上任一点将如何运动呢?其v,a如何计算呢?本章将用点的合成运动的方法来研究这类问题。
 §8-1相对运动·牵连运动·绝对运动
§8-1相对运动·牵连运动·绝对运动
1.定坐标系
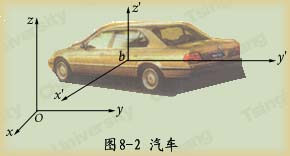
建立在固定参考物上的坐标系,简称定系。一般将定系固结在地面上。图8-2所示,是研究汽车相对于地面即![]() 坐标系的运动。
坐标系的运动。
2.动坐标系
动坐标系指建立在相对于定系运动着的物体上的坐标系,简称动系,如图8-2中的![]() 。有时可称为载体系。
。有时可称为载体系。
汽车车厢相对于![]() 在运动,如果将
在运动,如果将![]() 坐标系固结于车厢上,则形成了相对于定系
坐标系固结于车厢上,则形成了相对于定系![]() 有运动的坐标系。
有运动的坐标系。
3.动点
动点是指相对于定系和动系均有运动的点.本章就是研究动点相对于定系和动系的运动。如图8-2中任选车轮上的一点作为动点。
4.动点的绝对运动·绝对速度和绝对加速度
(1)绝对运动:动点相对于定系的运动。
(2)绝对速度:动点绝对运动的速度,用va表示。
(3)绝对加速度:动点绝对运动的加速度,用aa表示。
在第六章研究的点的运动学,即为绝对运动。演示动画8-1,观察转子轮缘上某点的绝对运动。
5.动点的相对运动·相对速度和相对加速度
(1)相对运动:动点相对于动系的运动。
(2)相对速度:动点相对运动的速度,用vr表示。
(3)相对加速度:动点相对运动的加速度,用ar表示。
6.牵连运动
动系相对于定系的运动称为牵连运动。
注意:动系作为一个整体运动着,因此,牵连运动具有刚体运动的特点,如平动或定轴转动。切勿称“动点的牵连运动”。
常选的动系多为平动动系或定轴转动动系。因此,常见的牵连运动形式即为平动或定轴转动。
7.动点的牵连速度和牵连加速度
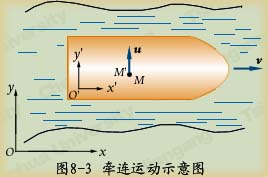
观察图8-3(下页),一船在水中以速度v航行。甲板上一人![]() 沿船横向运动,相对于船甲板的速度为u。若在岸上建立定系
沿船横向运动,相对于船甲板的速度为u。若在岸上建立定系![]() ,在甲板上建立动系
,在甲板上建立动系![]() 。则点的相对速度为
。则点的相对速度为![]() ,牵连运动作平动,那么动点的牵连速度如何分析呢?
,牵连运动作平动,那么动点的牵连速度如何分析呢?
(1)牵连点的概念
此时船是载体,每一瞬时人处于船上的某一点,此时![]() 所处位置记作
所处位置记作![]() 。
。
定义:任一瞬时,动系上与动点![]() 重合的点
重合的点![]() 即为此瞬时动点
即为此瞬时动点![]() 的牵连点。
的牵连点。
因此,牵连点是指动系上的点,动点运动到动系上的哪一点,该点就是动点的牵连点。
 (2)牵连速度
(2)牵连速度
定义:某瞬时牵连点的速度称为动点的牵连速度。用ve表示。
换句话说,如果此瞬时,动点站在甲板M’处不再作运动,则动点将随同M’点以相同的速度(相对于定系)运动。
因牵连运动指动系相对于定系而言,所以牵连速度亦是相对于定系而言。
图8-3中,船作平动,故牵连运动是平动,由§7-1知,平动刚体上各点速度相同,故动点的牵连速度![]() 。
。
(3)牵连加速度
定义:某瞬时牵连点的加速度称为动点的牵连加速度,用![]() 表示。
表示。
图8-3中若设v大小方向不变,则点M的![]() 。牵连加速度亦是相对于定系而言。
。牵连加速度亦是相对于定系而言。
8.运动方程及坐标变换
 可以利用坐标变换来建立绝对、相对和牵连运动之间的关系。以二维问题为例。设定系
可以利用坐标变换来建立绝对、相对和牵连运动之间的关系。以二维问题为例。设定系![]() ,动系
,动系![]() 。动点
。动点![]() ,如图8-4所示。
,如图8-4所示。
(1)绝对运动方程为:
![]() ,
,![]()
(2)相对运动方程为:
![]() ,
,![]()
(3)牵连运动的方程为:
![]() ,
,![]() ,
,![]()
由图8-4不难得到坐标变换关系:
 (8-1)
(8-1)
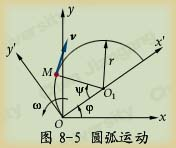
例8-1 点M相对于动系![]() 沿半径为
沿半径为![]() 的圆周以速度v作匀速圆周运动(圆心为
的圆周以速度v作匀速圆周运动(圆心为![]() ),动系
),动系![]() 相对于定系
相对于定系![]() 以匀角速度
以匀角速度![]() 绕
绕![]() 点作定轴转动,如图示。初始时
点作定轴转动,如图示。初始时![]() 与
与![]() 重合,点
重合,点![]() 与
与![]() 重合。试求点
重合。试求点![]() 的绝对运动方程。
的绝对运动方程。
解:连接![]() ,由图8-5可知:
,由图8-5可知: ![]()
 于是得点
于是得点![]() 的相对运动方程为
的相对运动方程为
![]()
![]()
牵连运动的方程为:
![]() ,
,![]() ,
,![]()
利用坐标变换关系式(8-1),得点M的绝对运动方程为
![]()
![]()
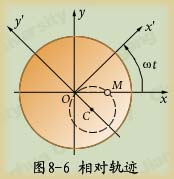
例8-2 用车刀切削工件的端面,车刀刀尖M沿水平轴x作往复运动,如图8-6所示。设![]() 为定坐标系,刀尖的运动方程为
为定坐标系,刀尖的运动方程为![]() 。工件以等角速度
。工件以等角速度![]() 逆时针方向转动。求车刀在工件圆端面上切出的痕迹。
逆时针方向转动。求车刀在工件圆端面上切出的痕迹。
解:根据题意,需求车刀刀尖M相对于工件的轨迹方程。
设刀尖M为动点,动系固定在工件上。则动点![]() 在动系
在动系![]() 和定系
和定系![]() 中的坐标关系为:
中的坐标关系为:
![]()
![]()
将点M的绝对运动方程代入上式中,得:
![]()
![]()
上式就是车刀相对于工件的运动方程。
从上式中消去时间t,得刀尖的相对轨迹方程
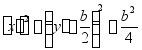
可见,车刀在工件上切出的痕迹是一个半径为![]() 的圆,该圆的圆心
的圆,该圆的圆心![]() 在动坐标轴
在动坐标轴![]() 上,圆周通过工件的中心
上,圆周通过工件的中心![]() 。
。
§ 8-2 点的速度合成定理
定理:某瞬时动点的绝对速度等于该瞬时动点的相对速度和牵连速度之矢量和。
即 ![]() (8-2)
(8-2)
证:1. 几何法
如图8-7所示一板![]() 上开槽,动点
上开槽,动点![]() 一方面沿槽相对于板运动,同时跟随板运动。板
一方面沿槽相对于板运动,同时跟随板运动。板![]() 即载体。设
即载体。设![]() 瞬时点
瞬时点![]() 与板上点
与板上点![]() 重合,经过△t瞬时后,
重合,经过△t瞬时后,![]() 板运动到
板运动到![]() 处,
处,![]() 沿
沿![]() 运动到
运动到![]() ,
,![]() 沿
沿![]() 运动到
运动到![]() 。
。
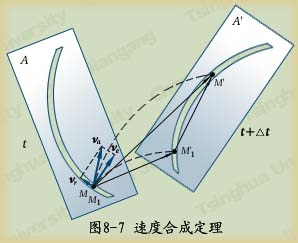 则:
则:![]() 为动点M的绝对轨迹,
为动点M的绝对轨迹,![]() 为绝对位移。
为绝对位移。
![]() 为动点M的相对轨迹,
为动点M的相对轨迹,![]() 为相对位移。
为相对位移。
![]() 为牵连点的轨迹,
为牵连点的轨迹,![]() 为牵连位移。
为牵连位移。
于是有:
![]()
推之: ![]()
当![]() 时,取极限
时,取极限
![]()
即 ![]() (8-2)
(8-2)
 如图8-7所示。
如图8-7所示。
2.解析法
(1)平动动系情形。如图8-8所示。
设:定系为![]() ,平动动系为
,平动动系为![]() ,动点
,动点![]() ,绝对矢径rM,相对矢径r,动系原点
,绝对矢径rM,相对矢径r,动系原点![]() 的位置由rA确定。有如下关系式:
的位置由rA确定。有如下关系式:
![]() (8-3)
(8-3)
![]() (8-4)
(8-4)
因动系作平动,i’,j’和k’大小、方向均不变。
∴ ![]() (8-5)
(8-5)
又平动刚体上各点速度相同,则
 (8-6)
(8-6)
∴ ![]() ——速度合成定理
——速度合成定理
(2)定轴转动动系情形。如图8-9所示
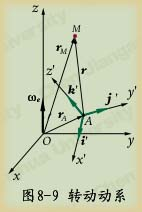 设:定系
设:定系![]() ;动系
;动系![]() ,绕
,绕![]() 轴作定轴转动,角速度为��������e ;动点M;绝对矢径rM;相对矢径r;动系原点矢径rA。仍有如下关系式:
轴作定轴转动,角速度为��������e ;动点M;绝对矢径rM;相对矢径r;动系原点矢径rA。仍有如下关系式:
![]() (8-3)
(8-3)
![]() (8-4)
(8-4)
![]() (8-5)
(8-5)
注意:此时动系上单位矢量i’,j’和k’方向随动系转动而变。且牵连点的速度不再等于vA 。因此:
![]()
![]() (8-7)
(8-7)
(3)绝对导数与相对导数的概念
① 相对导数
站在动坐标系来观察r随时间的变化率,相对于动系,i’,j’和k’方向是不变的(见上页图8-9)。所以的相对导数为:
![]() (8-7)′
(8-7)′
② 绝对导数
站在定系观察r的变化,就包含了i’,j’和k’方向的变化(动画演示)。因此式(8-7)是r的绝对导数。
∴ ![]() (8-8)
(8-8)
由§7-4,3。知: 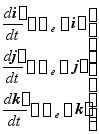 (8-9)
(8-9)
∴ ![]() (8-10)
(8-10)
将式(8-7)′,(8-10)代入式(8-5)有:
![]() (8-11)
(8-11)
 又因动系作定轴转动,由式(7-15)知
又因动系作定轴转动,由式(7-15)知
![]()
∴ 式(8-11)改写成:
![]()
由图8-9可知:![]() 代表动系上牵连点的速度ve。
代表动系上牵连点的速度ve。
∴ ![]() ——速度合成定理
——速度合成定理
证毕。
例8-3刨床的急回机构如图8-10所示。曲柄![]() 的一端
的一端![]() 与滑块用铰链连接。当曲柄
与滑块用铰链连接。当曲柄![]() 以匀角速度
以匀角速度![]() 绕固定轴
绕固定轴![]() 转动时,滑块在摇杆
转动时,滑块在摇杆![]() 上滑动,并带动摇杆
上滑动,并带动摇杆![]() 绕固定轴
绕固定轴![]() 摆动。设曲柄长
摆动。设曲柄长![]() ,两轴间的距离
,两轴间的距离![]() 。求当曲柄在水平位置时摇杆的角速度
。求当曲柄在水平位置时摇杆的角速度![]() 。
。
解:在本题中应选取曲柄端点![]() 作为研究的动点,把动系
作为研究的动点,把动系![]() 固定在摇杆
固定在摇杆![]() 上,并与
上,并与![]() 一起绕
一起绕![]() 轴摆动。
轴摆动。
点的绝对运动是以点![]() 为圆心的圆周运动,相对运动是沿
为圆心的圆周运动,相对运动是沿![]() 方向的直线运动,而牵连运动则是摇杆绕
方向的直线运动,而牵连运动则是摇杆绕![]() 轴的摆动。
轴的摆动。
于是,绝对速度va的大小和方向都是已知的,它的大小等于![]() ,而方向与曲柄
,而方向与曲柄![]() 垂直;相对速度vr的方向是已知的,即沿
垂直;相对速度vr的方向是已知的,即沿![]() ;而牵连速度ve是杆
;而牵连速度ve是杆![]() 上与点
上与点![]() 重合的那一点的速度,它的方向垂直于
重合的那一点的速度,它的方向垂直于![]() ,也是已知的。共计有四个要素已知。由于
,也是已知的。共计有四个要素已知。由于![]() 的大小和方向都已知,因此,这是一个速度分解的问题。
的大小和方向都已知,因此,这是一个速度分解的问题。
作出速度四边形,如图8-10所示。由其中的直角三角形可求得

![]()
又 ![]() ,且
,且![]() ,
,
所以 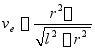
设摇杆在此瞬时的角速度为��������1,则

其中 ![]() 。
。
 由此得出此瞬时摇杆的角速度为
由此得出此瞬时摇杆的角速度为
![]() 方向如图。
方向如图。
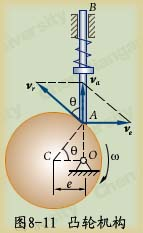
例8-4如图8-11所示,半径为![]() 、偏心距为
、偏心距为![]() 的凸轮,以匀角速度
的凸轮,以匀角速度![]() 绕
绕![]() 轴转动,杆
轴转动,杆![]() 能在滑槽中上下平动,杆的端点A始终与凸轮接触,且
能在滑槽中上下平动,杆的端点A始终与凸轮接触,且![]() 成一直线。求在图示位置时,杆
成一直线。求在图示位置时,杆![]() 的速度。
的速度。
解:因为杆AB作平动,各点速度相同,因此只要求出其上任一点的速度即可。选取杆AB的端点A作为研究的动点,动系随凸轮一起绕O轴转动。
点A的绝对运动是直线运动,相对运动是以凸轮中心C为圆心的圆周运动,牵连运动则是凸轮绕O轴的转动。
于是,绝对速度方向沿AB,相对速度方向沿凸轮圆周的切线,而牵连速度为凸轮上与杆端A点重合的那一点的速度,它的方向垂直于OA,它的大小为![]() 。根据速度合成定理,已知四个要素,即可作出速度平行四边形,如图所示。由三角关系求得杆的绝对速度为
。根据速度合成定理,已知四个要素,即可作出速度平行四边形,如图所示。由三角关系求得杆的绝对速度为
![]()
例8-5矿砂从传送带A落到另一传送带B上,如图8-12(a)所示。站在地面上观察矿砂下落的速度为![]() ,方向与铅直线成
,方向与铅直线成![]() 角。已知传送带B水平传动速度
角。已知传送带B水平传动速度![]() 。求矿砂相对于传送带B的速度。
。求矿砂相对于传送带B的速度。
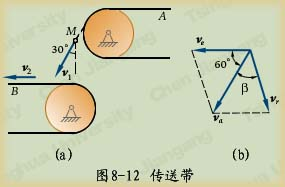 解:以矿砂M为动点,动系固定在传送带B上。矿砂相对地面的速度v1为绝对速度;牵连速度应为动参考系上与动点相重合的那一点的速度。可设想动参考系为无限大,由于它作平动,各点速度都等于v2。于是v2等于动点M的牵连速度。
解:以矿砂M为动点,动系固定在传送带B上。矿砂相对地面的速度v1为绝对速度;牵连速度应为动参考系上与动点相重合的那一点的速度。可设想动参考系为无限大,由于它作平动,各点速度都等于v2。于是v2等于动点M的牵连速度。
由速度合成定理知,三种速度形成平行四边形,绝对速度必须是对角线,因此作出的速度平行四边形如图8-12(b)所示。根据几何关系求得
![]() m/s
m/s
vr与va间的夹角为 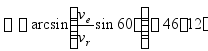
§8-3 点的加速度合成定理
1.平动动系情形下的加速度合成定理
![]() (8-12)
(8-12)
 证:由图8-8及式(8-2)~(8-6):
证:由图8-8及式(8-2)~(8-6):
![]()
![]() (平动动系上各点加速度相同)
(平动动系上各点加速度相同)
![]() (i′,j′,k′方向不变)
(i′,j′,k′方向不变)
证得 ![]()
2.转动动系情形下的加速度合成定理
![]() (8-13)
(8-13)
其中 ![]() (8-14)
(8-14)
��������e——动系的角速度
 证:仍采用两种方法。
证:仍采用两种方法。
1.几何法
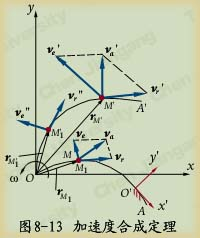
不失一般性,我们讨论一特例如图8-13所示。
设一曲杆OA绕O轴转动,角速度为![]() ;动点M沿OA运动。
;动点M沿OA运动。
现分析点M的加速度。动系固结于OA上,则牵连角速度![]() 。设t瞬时点M位于OA上之M1点,此时的相对速度为vr,牵连速度为ve。根据速度合成定理(见§8-2)有:
。设t瞬时点M位于OA上之M1点,此时的相对速度为vr,牵连速度为ve。根据速度合成定理(见§8-2)有:
![]()
经过△t之后,![]() 运动到
运动到![]() ;点
;点![]() 运动到
运动到![]() ;点
;点![]() 运动到
运动到![]() 。
。
![]() ;
; ![]() ;
;![]()
有 ![]() (8-15)
(8-15)
设此时![]() 之速度为
之速度为![]() ,t瞬时记录在动系上的相对速度vr由于牵连运动而变为
,t瞬时记录在动系上的相对速度vr由于牵连运动而变为![]() (见动画8-5)。根据加速度的定义,有:
(见动画8-5)。根据加速度的定义,有:
![]() (8-16)
(8-16)
相对加速度 ![]() (相对于动系观察vr之变化) (8-17)
(相对于动系观察vr之变化) (8-17)
牵连加速度 ![]() (牵连点的加速度) (8-18)
(牵连点的加速度) (8-18)
考虑式(8-17)和(8-18),则式(8-16)写成:
![]()
![]() (8-19)
(8-19)
其中 ![]()
![]()
又 ∵ ![]() ,回顾§7-4.3,有
,回顾§7-4.3,有
![]() (8-20)
(8-20)
回顾式(7-15),有:
![]() ,
, ![]()
∴ ![]()
于是:
![]() (8-21)
(8-21)
将式(8-20),(8-21)代入式(8-19),则证明了加速度合成定理。
![]()
其中![]() 称为科氏加速度。
称为科氏加速度。
讨论:![]() 的物理意义:
的物理意义:
(1)![]() ,反映由于牵连运动(转动)引起相对速度方向之变化率。在动系上看不见这个变化。
,反映由于牵连运动(转动)引起相对速度方向之变化率。在动系上看不见这个变化。
(2)![]() ,反映由于相对运动引起牵连速度大小的变化率。
,反映由于相对运动引起牵连速度大小的变化率。
牵连加速度应比较t和t+△t两瞬时牵连点M1的速度之变化,即![]() ,但由于相对运动的存在,t+△t瞬时之牵连速度为
,但由于相对运动的存在,t+△t瞬时之牵连速度为![]() 了,此时已非t瞬时牵连点了。
了,此时已非t瞬时牵连点了。
 2.解析法
2.解析法
观察图8-9
![]()
![]() (8-22)
(8-22)
(1) ![]() (见式(8-6))
(见式(8-6))
∴ ![]()
![]() (参见式(8-9),(8-6)) (8-23)
(参见式(8-9),(8-6)) (8-23)
其中 ![]() 为相对加速度。相对于动系,i′、j′、k′方向不变,只有
为相对加速度。相对于动系,i′、j′、k′方向不变,只有![]() ,
,![]() ,
,![]() 变化,因此亦可写作:
变化,因此亦可写作:
![]() (8-24)
(8-24)
![]() 项反映由于牵连运动(转动)引起vr方向之变化。
项反映由于牵连运动(转动)引起vr方向之变化。
(2)![]()
∴ ![]()
![]()
![]() (8-25)
(8-25)
其中,![]() (牵连加速度);此式中的
(牵连加速度);此式中的![]() 反映相对运动引起的ve大小的改变,将式(8-23),(8-25)代入(8-22)得:
反映相对运动引起的ve大小的改变,将式(8-23),(8-25)代入(8-22)得:
![]()
其中 ![]()
证毕。
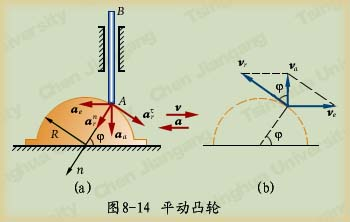 例8-6凸轮在水平面上向右作减速运动,如图8-14a所示。设凸轮半径为R,图示瞬时的速度和加速度分别为v和a。求杆AB在图示位置时的加速度。
例8-6凸轮在水平面上向右作减速运动,如图8-14a所示。设凸轮半径为R,图示瞬时的速度和加速度分别为v和a。求杆AB在图示位置时的加速度。
解:以杆AB上的点A为动点,凸轮为动系,则点A的绝对轨迹为直线,相对轨迹为凸轮轮廓曲线。由于牵连运动为平动,点的加速度合成定理为
![]()
式中aa为所求的加速度,已知它的方向沿直线AB,但指向和大小尚待确定。
点A的牵连加速度为凸轮上与动点重合的那一点的加速度,即
![]()
点A的相对轨迹为曲线,于是相对加速度分为两个分量:切向分量![]() 的大小是未知的,法向分量
的大小是未知的,法向分量![]() 的方向如图所示,大小为
的方向如图所示,大小为
![]()
式中vr的相对速度可根据速度合成定理求出,它的方向如图(b)所示,大小为
![]()
于是 ![]()
加速度合成定理可写成如下形式:
![]()
假设aa和![]() 的指向如图所示。为计算aa的大小,将上式投影到法线上,得
的指向如图所示。为计算aa的大小,将上式投影到法线上,得
![]()
解得 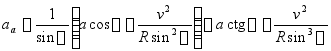
当![]() 时,
时,![]() ,说明假设的aa的指向恰是其真实指向。
,说明假设的aa的指向恰是其真实指向。
 例8-7刨床的急回机构如图8-15所示。曲柄OA的一端A与滑块用铰链连接。当曲柄OA以匀角速度
例8-7刨床的急回机构如图8-15所示。曲柄OA的一端A与滑块用铰链连接。当曲柄OA以匀角速度![]() 绕固定轴O转动时,滑块在摇杆O1B上滑动,并带动摇杆O1B绕固定轴O1摆动。设曲柄长
绕固定轴O转动时,滑块在摇杆O1B上滑动,并带动摇杆O1B绕固定轴O1摆动。设曲柄长![]() ,两轴间的距离
,两轴间的距离![]() 。求当曲柄在水平位置时摇杆的角加速度。
。求当曲柄在水平位置时摇杆的角加速度。
解:在本题中应选取曲柄端点A作为研究的动点,把动系![]() 固定在摇杆O1B上,并与O1B一起绕O1轴摆动。因动系作转动,因此加速度合成定理为
固定在摇杆O1B上,并与O1B一起绕O1轴摆动。因动系作转动,因此加速度合成定理为
![]()
由于![]() ,欲求摇杆O1B的角加速度
,欲求摇杆O1B的角加速度![]() ,只需求出
,只需求出![]() 即可。
即可。
现在分别分析上式中的各项:
![]() :因为动点的绝对运动是以O为圆心的匀速圆周运动,故只有法向加速度,方向如图所示,大小为
:因为动点的绝对运动是以O为圆心的匀速圆周运动,故只有法向加速度,方向如图所示,大小为![]() ;
;
![]() :摇杆上与动点相重合的那一点的加速度。摇杆摆动,其上点A的切向加速度为
:摇杆上与动点相重合的那一点的加速度。摇杆摆动,其上点A的切向加速度为![]() ,垂直于O1A,假设指向如图;法向加速度为
,垂直于O1A,假设指向如图;法向加速度为![]() ,它的大小为
,它的大小为![]() 方向如图所示。在前例8-3中已求得
方向如图所示。在前例8-3中已求得
![]() ,且
,且![]()
 固有:
固有: 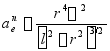
![]() :因相对轨迹为直线,故
:因相对轨迹为直线,故![]() 沿O1A,大小未知。
沿O1A,大小未知。
![]() :由
:由![]() 知
知![]() ,由前例8-3知
,由前例8-3知
![]()
于是有
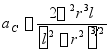
方向如图所示。
为了求得![]() ,应将加速度合成定理向
,应将加速度合成定理向![]() 轴投影,即:
轴投影,即:

![]()
或 ![]()
解得
![]()
式中![]() ,故
,故![]() 为负值。负号表示真实方向与图中假设的指向相反。
为负值。负号表示真实方向与图中假设的指向相反。
摇杆O1A的角加速度
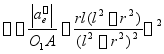
方向如图示。
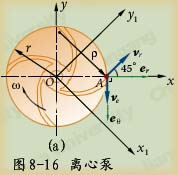 例8-8如图8-16(a)所示一离心泵的工作叶轮,它以匀转速
例8-8如图8-16(a)所示一离心泵的工作叶轮,它以匀转速![]() 顺时针转向转动。设流体质点A在叶轮出口处的绝对速度的径向分量
顺时针转向转动。设流体质点A在叶轮出口处的绝对速度的径向分量![]() 。在叶轮出口处,质点相对切向加速度大小为24m/s2,方向如图(b)所示。已知叶轮的导流曲线在出口处的曲率半径为
。在叶轮出口处,质点相对切向加速度大小为24m/s2,方向如图(b)所示。已知叶轮的导流曲线在出口处的曲率半径为![]() m,且切口处切线与半径成
m,且切口处切线与半径成![]() 角。叶轮半径
角。叶轮半径![]() 。试求流体质点在出口处的绝对加速度。
。试求流体质点在出口处的绝对加速度。
解:选叶轮出口处的流体质点A为研究对象。作定系![]() ,动系
,动系![]() 固结在叶轮上。画出A点的相对速度vr和牵连速度ve如图所示。
固结在叶轮上。画出A点的相对速度vr和牵连速度ve如图所示。
设er表示径向单位矢量。根据速度合成定理![]() ,将速度矢量式投影于径向,vr0表示v在径向的投影,得
,将速度矢量式投影于径向,vr0表示v在径向的投影,得
![]()
因题设![]() ,于是得到A点的相对速度为
,于是得到A点的相对速度为
![]()
根据动坐标系为转动时的加速度合成定理,有
![]()
其中:![]() 的方向指向叶轮中心,大小为
的方向指向叶轮中心,大小为

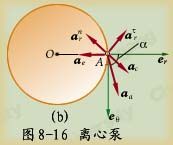 因
因![]() 点的相对运动为曲线运动,
点的相对运动为曲线运动,![]() 可分解成相对切向及相对法向加速度两部分,即
可分解成相对切向及相对法向加速度两部分,即
![]()
![]()
![]() 沿叶片出口处的切线方向与点径向成
沿叶片出口处的切线方向与点径向成![]() 角,大小为
角,大小为![]() ;
;![]() 的方向垂直于
的方向垂直于![]() ,指向叶片出口处导流曲线的曲率中心,大小为
,指向叶片出口处导流曲线的曲率中心,大小为
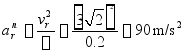 。
。
aC的方向垂直于![]() ,指向与
,指向与![]() 相反,大小为
相反,大小为
![]() m/s2。
m/s2。
画出各加速度分量如图(b)所示。
设![]() 表示横向单位矢量。现利用各加速度分量在径向
表示横向单位矢量。现利用各加速度分量在径向![]() 和横向
和横向![]() 的投影
的投影![]() 和
和![]() 来计算绝对加速度,得到:
来计算绝对加速度,得到:
![]()
![]()
![]() m/s2
m/s2
![]()
![]()
![]() m/s2
m/s2
A点的绝对加速度的大小为
![]()
![]() m/s,
m/s,
其方向为![]()
![]()